��Ŀ����
14����֪����A����Բ C��$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0���ϣ�����B��ֱ�� x=-2�ϣ������� $\overrightarrow{OA}$��$\overrightarrow{OB}$��OΪ����ԭ�㣩����ԲC�ϵ� $M��\frac{{\sqrt{3}}}{2}��3��$�����������֮��Ϊ 4$\sqrt{3}$��������ԲC���̣�
�����ж�ֱ��AB��Բx2+y2=3��λ�ù�ϵ����֤����Ľ��ۣ�
���� ���������⣬$\left\{\begin{array}{l}{2a=4\sqrt{3}}\\{\frac{9}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\end{array}\right.$�����a��b����������ԲC���̣�
���������A��B������ֱ�Ϊ��x0��y������-2��t����ֱ��AB�ķ���Ϊ��y0-t��x-��x0+2��y+��tx0+2y0��=0����OA��OB�õ�t=$\frac{2{x}_{0}}{{y}_{0}}$��Ȼ����Բx2+y2=3��Բ�ĵ�AB�ľ����Բ�İ뾶���˵��ֱ��AB��Բx2+y2=3���У�
��� �⣺���������⣬$\left\{\begin{array}{l}{2a=4\sqrt{3}}\\{\frac{9}{{a}^{2}}+\frac{3}{4{b}^{2}}=1}\end{array}\right.$��
��a=2$\sqrt{3}$��b=$\sqrt{3}$��
����ԲC����Ϊ$\frac{{y}^{2}}{12}+\frac{{x}^{2}}{3}=1$��
����ֱ��AB��Բx2+y2=3���У�
֤�����£�
���A��B������ֱ�Ϊ��x0��y0������-2��t����ֱ��AB�ķ���Ϊ��y0-t��x-��x0+2��y+��tx0+2y0��=0��
��OA��OB��
��$\overrightarrow{OA}$•$\overrightarrow{OB}$=0����-2x0+ty0=0�����t=$\frac{2{x}_{0}}{{y}_{0}}$��
Բ��O��ֱ��AB�ľ���d=$\frac{|t{x}_{0}+2{y}_{0}|}{\sqrt{��{y}_{0}-t��^{2}+��{x}_{0}+2��^{2}}}$=$\frac{6|4-{{x}_{0}}^{2}|}{\sqrt{12��{{x}_{0}}^{4}-8{{x}_{0}}^{2}+16��}}$=$\sqrt{3}$
��ֱ��AB��Բx2+y2=3���У�
���� ���⿼����Բ�ļ������ʣ�������Բ��Բ���ߵ��ۺϣ�ѵ������Բ�ĵ�ֱ�ߵľ����ж�ֱ�ߺ�Բ��λ�ù�ϵ����������������������������������⣮

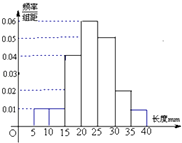 ij�ij�Ϊ���˽�һ���������������������ȡ��100������ά�ij��ȣ�����ά�ij���������������Ҫָ�꣩���������ݶ�������[5��40]�У���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���ӳ�����100������ά�������ȡһ������������ά�ij���С��20mm�ĸ����ǣ�������
ij�ij�Ϊ���˽�һ���������������������ȡ��100������ά�ij��ȣ�����ά�ij���������������Ҫָ�꣩���������ݶ�������[5��40]�У���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���ӳ�����100������ά�������ȡһ������������ά�ij���С��20mm�ĸ����ǣ�������| A�� | $\frac{3}{10}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{3}{8}$ | D�� | $\frac{3}{5}$ |
| A�� | ��-1��2�� | B�� | ��-2��1�� | C�� | ��-2��+�ޣ� | D�� | ��-1��+�ޣ� |
| A�� | c��b��a | B�� | a��b��c | C�� | b��a��c | D�� | b��c��a |
 ij�������ȡ������ҵ�������Ͻ�˰���������λ����Ԫ�������������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������Ͻ�˰�շ�Χ��[0��100]���������ݷ���Ϊ[0��20����[20��40����[40��60����[60��80����[80��100]��
ij�������ȡ������ҵ�������Ͻ�˰���������λ����Ԫ�������������ݻ��Ƴ�Ƶ�ʷֲ�ֱ��ͼ����ͼ�������Ͻ�˰�շ�Χ��[0��100]���������ݷ���Ϊ[0��20����[20��40����[40��60����[60��80����[80��100]��