题目内容
已知圆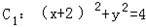 及点C2(2,0),在圆
及点C2(2,0),在圆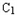 上任取一点P,连接C2P,做线段C2P的中垂线交直线
上任取一点P,连接C2P,做线段C2P的中垂线交直线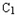 P于点M.
P于点M.
(1)当点P在圆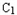 上运动时,求点M的轨迹E的方程;
上运动时,求点M的轨迹E的方程;
(2)设轨迹E与x轴交于 ,A2两点,在轨迹E上任取一点Q(
,A2两点,在轨迹E上任取一点Q(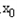 ,
,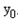 )(
)(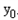 ≠0),直线Q
≠0),直线Q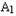 ,QA2分别交y轴于D,E两点,求证:以线段DE为直径的圆C过两个定点,并求出定点坐标.
,QA2分别交y轴于D,E两点,求证:以线段DE为直径的圆C过两个定点,并求出定点坐标.
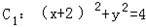 及点C2(2,0),在圆
及点C2(2,0),在圆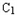 上任取一点P,连接C2P,做线段C2P的中垂线交直线
上任取一点P,连接C2P,做线段C2P的中垂线交直线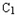 P于点M.
P于点M.(1)当点P在圆
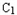 上运动时,求点M的轨迹E的方程;
上运动时,求点M的轨迹E的方程;(2)设轨迹E与x轴交于
 ,A2两点,在轨迹E上任取一点Q(
,A2两点,在轨迹E上任取一点Q(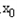 ,
,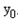 )(
)(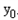 ≠0),直线Q
≠0),直线Q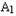 ,QA2分别交y轴于D,E两点,求证:以线段DE为直径的圆C过两个定点,并求出定点坐标.
,QA2分别交y轴于D,E两点,求证:以线段DE为直径的圆C过两个定点,并求出定点坐标.(1)解:∵线段C2P的中垂线交直线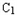 P于点M,
P于点M,
∴|MC2|=|MP|,
又∵|MP|=|M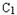 |+2,
|+2,
∴|M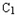 |﹣|MC2|=±2(2<4)
|﹣|MC2|=±2(2<4)
∴M点轨迹是以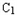 ,C2为焦点的双曲线,且2a=2,2c=4
,C2为焦点的双曲线,且2a=2,2c=4
∴点M的轨迹E的方程为
(2)证明: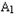 (﹣1,0),A2(1,0),
(﹣1,0),A2(1,0),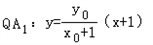 ,
,
∴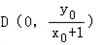
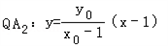 ,
,
∴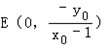
∴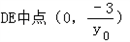
∴以DE为直径的圆方程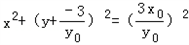
∴y=0时,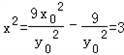
∴以线段DE为直径的圆C过两个定点,定点为
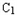 P于点M,
P于点M,∴|MC2|=|MP|,
又∵|MP|=|M
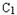 |+2,
|+2,∴|M
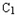 |﹣|MC2|=±2(2<4)
|﹣|MC2|=±2(2<4)∴M点轨迹是以
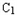 ,C2为焦点的双曲线,且2a=2,2c=4
,C2为焦点的双曲线,且2a=2,2c=4∴点M的轨迹E的方程为

(2)证明:
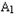 (﹣1,0),A2(1,0),
(﹣1,0),A2(1,0),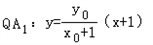 ,
,∴
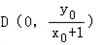
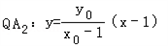 ,
,∴
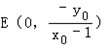
∴
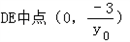
∴以DE为直径的圆方程
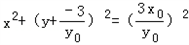
∴y=0时,
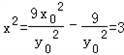
∴以线段DE为直径的圆C过两个定点,定点为


练习册系列答案
相关题目
 及点C2(2,0),在圆
及点C2(2,0),在圆 上任取一点P,连接C2P,做线段C2P的中垂线交直线
上任取一点P,连接C2P,做线段C2P的中垂线交直线 P于点M.
P于点M.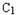 上运动时,求点M的轨迹E的方程;
上运动时,求点M的轨迹E的方程; ,A2两点,在轨迹E上任取一点Q(x0,y0)(y0≠0),直线Q
,A2两点,在轨迹E上任取一点Q(x0,y0)(y0≠0),直线Q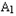 ,QA2分别交y轴于D,E两点,求证:以线段DE为直径的圆C过两个定点,并求出定点坐标.
,QA2分别交y轴于D,E两点,求证:以线段DE为直径的圆C过两个定点,并求出定点坐标. 及点C2(2,0),在圆C1上任取一点P,连接C2P,做线段C2P的中垂线交直线C1P于点M.
及点C2(2,0),在圆C1上任取一点P,连接C2P,做线段C2P的中垂线交直线C1P于点M. 及点C2(2,0),在圆C1上任取一点P,连接C2P,做线段C2P的中垂线交直线C1P于点M.
及点C2(2,0),在圆C1上任取一点P,连接C2P,做线段C2P的中垂线交直线C1P于点M.