题目内容
已知奇函数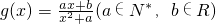 的定义域为R,且恒有
的定义域为R,且恒有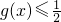 .
.
(1)求a,b的值;
(2)写出函数y=g(x)在[-1,1]上的单调性,并用定义证明;
(3)讨论关于x的方程g(x)-t=0(t∈R)的根的个数.
解:(1)∵g(x)为奇函数且函数的定义域为R,
∴a>0且g(0)= =0
=0
∴b=0,故有g(x)=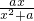
∵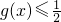 恒成立即
恒成立即 恒成立
恒成立
整理可得,x2-2ax+a≥0恒成立
∴△=4a2-4a≤0
解可得,0<a≤1
∵a∈N*
∴a=1
(2)g(x)在[-1,1]上单调递增,证明如下
z证明:由(1)可得,g(x)= ,x∈[-1,1]
,x∈[-1,1]
设0≤x1<x2≤1
则g(x1)-g(x2)=
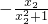
=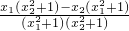
=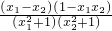
∵0≤x1<x2≤1
∴x1-x2<0,1-x1x2>0,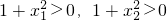
则g(x1)-g(x2)=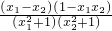 <0
<0
即g(x1)<g(x2)
∴g(x)在[0,1]上单调递增
根据奇函数对称区间上的单调性一致可知,且g(0)=0,则可得g(x)在[-1,0)上单调递增
综上可得,g(x)在[-1,1]上单调递增
(3)由(2)可得,-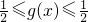
①当t 或t
或t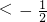 时,方程g(x)-t=0没有实数根
时,方程g(x)-t=0没有实数根
②当-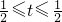 时,方程g(x)-t=0有1根实数根
时,方程g(x)-t=0有1根实数根
分析:(1)由g(x)为奇函数且函数的定义域为R,可知a>0且g(0)=0可求b,然后由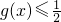 恒成立,结合二次函数性质及a∈N*可求a
恒成立,结合二次函数性质及a∈N*可求a
(2)可先证明g(x)= ,x∈[0,1]上的单调性,然后根据奇函数对称区间上的单调性一致可知,且g(0)=0,则可判断g(x)在[-1,0)上单调性
,x∈[0,1]上的单调性,然后根据奇函数对称区间上的单调性一致可知,且g(0)=0,则可判断g(x)在[-1,0)上单调性
(3)由(2)的函数的单调性可求g(x)的值域,即可判断方程的根的个数
点评:题主要考查方程的根的存在性及个数判断,求函数的解析式和单调区间,函数的奇偶性的应用,体现了化归与转化的数学思想,属于中档题.
∴a>0且g(0)=
 =0
=0∴b=0,故有g(x)=
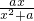
∵
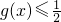 恒成立即
恒成立即 恒成立
恒成立整理可得,x2-2ax+a≥0恒成立
∴△=4a2-4a≤0
解可得,0<a≤1
∵a∈N*
∴a=1
(2)g(x)在[-1,1]上单调递增,证明如下
z证明:由(1)可得,g(x)=
 ,x∈[-1,1]
,x∈[-1,1]设0≤x1<x2≤1
则g(x1)-g(x2)=

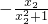
=
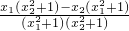
=
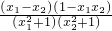
∵0≤x1<x2≤1
∴x1-x2<0,1-x1x2>0,
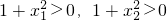
则g(x1)-g(x2)=
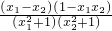 <0
<0即g(x1)<g(x2)
∴g(x)在[0,1]上单调递增
根据奇函数对称区间上的单调性一致可知,且g(0)=0,则可得g(x)在[-1,0)上单调递增
综上可得,g(x)在[-1,1]上单调递增
(3)由(2)可得,-
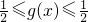
①当t
 或t
或t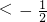 时,方程g(x)-t=0没有实数根
时,方程g(x)-t=0没有实数根②当-
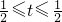 时,方程g(x)-t=0有1根实数根
时,方程g(x)-t=0有1根实数根分析:(1)由g(x)为奇函数且函数的定义域为R,可知a>0且g(0)=0可求b,然后由
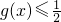 恒成立,结合二次函数性质及a∈N*可求a
恒成立,结合二次函数性质及a∈N*可求a(2)可先证明g(x)=
 ,x∈[0,1]上的单调性,然后根据奇函数对称区间上的单调性一致可知,且g(0)=0,则可判断g(x)在[-1,0)上单调性
,x∈[0,1]上的单调性,然后根据奇函数对称区间上的单调性一致可知,且g(0)=0,则可判断g(x)在[-1,0)上单调性(3)由(2)的函数的单调性可求g(x)的值域,即可判断方程的根的个数
点评:题主要考查方程的根的存在性及个数判断,求函数的解析式和单调区间,函数的奇偶性的应用,体现了化归与转化的数学思想,属于中档题.

练习册系列答案
相关题目
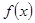 的定义域为
的定义域为 ,且
,且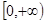 上是增函数, 是否存在实数
上是增函数, 是否存在实数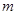 使得
使得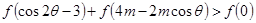 , 对一切
, 对一切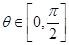
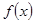 的定义域为
的定义域为 ,且
,且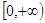 上是增函数, 是否存在实数
上是增函数, 是否存在实数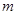 使得
使得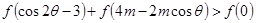 , 对一切
, 对一切 都成立?若存在,求出实数
都成立?若存在,求出实数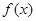 的定义域为
的定义域为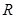 ,且是以2为周期的周期函数,数列
,且是以2为周期的周期函数,数列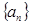 是首项为1,公差为1的等差数列,则
是首项为1,公差为1的等差数列,则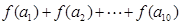 的值为 ( )
的值为 ( )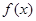 的定义域为
的定义域为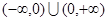 ,且在
,且在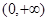 上为增函数,
上为增函数,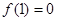 .
.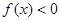 的解集;
的解集;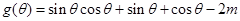 ,
,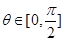 ,若不等式组
,若不等式组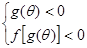 恒成立,
恒成立,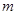 的取值范围.
的取值范围.