题目内容

12．设z=2x+y，其中变量x和y满足条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$，求z的最大值和最小值．

分析 作出不等式组对应的平面区域，利用目标函数的几何意义，求最值即可．

解答 解：作出可行域，如图…（4分）
作出直线y=-2x，并平移
当直线经过点C时z取最大值，解方程组$\left\{\begin{array}{l}{x+y=1}\\{y=-1}\end{array}\right.$，
得C（2，-1）…（6分）
此时最大值z=2×2-1=3…（7分）
当直线经过点B时，z取最小值，解方程组$\left\{\begin{array}{l}{y=x}\\{y=-1}\end{array}\right.$得B（-1，-1…（9分）
此时最小值z=-1×2-1=-3…（10分）

点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．

练习册系列答案
相关题目
2．已知函数f（x）=$\left\{\begin{array}{l}{{a}^{x}，x＜0}\\{（a-2）x+3a，x≥0}\end{array}\right.$满足对任意的x1≠x2，都有$\frac{f（{x}_{1}）-f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＜0成立，则a的取值范围是（0，$\frac{1}{3}$]．
3．经过（-1，2）且与直线x+y-1=0垂直的直线是（　　）
A．x-y+1=0B．x-y+3=0C．x+y+1=0D．x+y+3=0
20．福州为了迎接青运会，计划从2011年到2015年，每年年初投入资金用于更新和改进体育场所与设施，若2011年年初投入a万元，以后每年年初投入的资金比上一年递增10%，则投入的总资金约为（参考数据 1.14≈1.46，1.15≈1.61）（　　）
A．4.6a万元B．6.1a万元C．14.6a万元D．16.1a万元
7．已知正数数列{an}满足an+1=2an，则此数列{an}是（　　）
A．递增数列B．递减数列
C．常数列D．无法确定数列的增减性
17．sin 20°cos10°+cos20°sin170°=（　　）
A．-$\frac{\sqrt{3}}{2}$B．$\frac{\sqrt{3}}{2}$C．-$\frac{1}{2}$D．$\frac{1}{2}$
4．已知f（x）=$\left\{\begin{array}{l}{-x，-1≤x＜0}\\{{x}^{2}，0≤x＜1}\\{x，1≤x≤2}\end{array}\right.$
（1）求f（$\frac{3}{2}$），f[f （-$\frac{2}{3}$）]值；
（2）若f （x）=$\frac{1}{2}$，求x值；
（3）作出该函数简图（画在如图坐标系内）；
（4）求函数的单调增区间与值域．
1．已知函数f（x）=|x-3|-|x+1|，命题p：关于x的不等式f（x）＞a对x∈R恒成立；命题q：函数y=x2-ax+4在区间[5，+∞）上单调递增．
（1）解不等式f（x）≤0；
（2）若命题“p或q”是真命题，求实数a的取值范围．
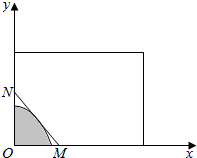2．如图，某房地产公司要在一块矩形宽阔地面上开发物业，阴影部分是不能开发的古建筑群，且要求用在一条直线上的栏栅进行隔离，古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分，栏栅与矩形区域边界交于点M，N．则△MON面积的最小值为$\frac{2}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网