题目内容
（12分）关于x的不等式|x－2|+|x－a|≥a在R上恒成立，求实数a的取值范围．
{a|a≤1}
（1）当a≤0时，不等式|x－2|+|x－a|≥a在R上恒成立；（2）当a>0时，由于|x－2|+|x－a|≥|2－a|，要使不等式|x－2|+|x－a|≥a恒成立，只要|2－a|≥a即可，
解得0<a≤1；综上（1）和（2）可知，实数a的取值范围为{a|a≤1}．
解得0<a≤1；综上（1）和（2）可知，实数a的取值范围为{a|a≤1}．
练习册系列答案
相关题目
.
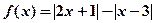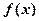≤4；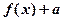
≤0成立，求实数a的取值范围. 
的解集为______________.
；
，恒有
成立，求
的取值范围．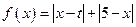
的最小值为3, 
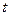的值是________.
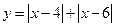的最小值为（ ）
