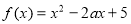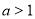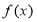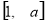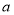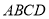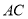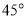题目内容
已知函数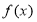 是定义在
是定义在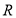 上的偶函数,当
上的偶函数,当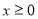 时,
时,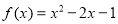 。
。
(1)求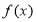 的函数解析式,并用分段函数的形式给出;
的函数解析式,并用分段函数的形式给出;
(2)作出函数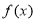 的简图;
的简图;
(3)写出函数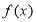 的单调区间及最值.
的单调区间及最值.
(1) ;
;
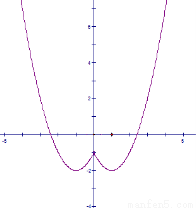
(2)如图
(3)单调增区间为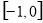 和
和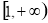 ,单调减区间为
,单调减区间为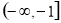 和
和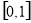 ,当
,当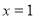 或
或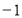 时,
时,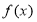 有最小值-2.
有最小值-2.
【解析】
试题分析:(1)当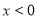 时,
时,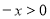 ,则
,则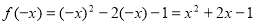 ,由偶函数的性质,
,由偶函数的性质,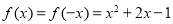 ,因此
,因此 .(3)由
.(3)由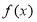 的图像可直接看出单调增区间为
的图像可直接看出单调增区间为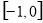 和
和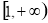 ,单调减区间为
,单调减区间为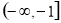 和
和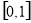 ,当
,当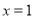 或
或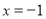 时,
时,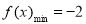 .
.
试题解析:(1)当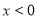 时,
时,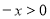 , 1分
, 1分
则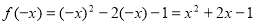 3分
3分
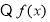 是偶函数
是偶函数 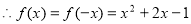 5分
5分
∴ . 6分
. 6分
(如果通过图象直接给对解析式得2分)
(2)函数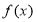 的简图:
的简图:
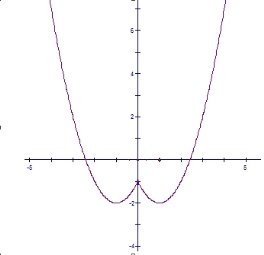 9分
9分
(3)单调增区间为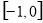 和
和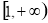 11分
11分
单调减区间为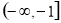 和
和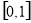 13分
13分
当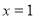 或
或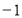 时,
时,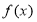 有最小值-2 . 15分
有最小值-2 . 15分
考点:1、偶函数的性质;2、函数的图像.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目