��Ŀ����
ijͬѧ��һ���о���ѧϰ�з��֣��������ʽ�ӵ�ֵ������ͬһ��������
��sin213�㣫cos217��-sin13��cos17�㣻
��sin215�㣫cos215��-sin15��cos15�㣻
��sin218�㣫cos212��-sin18��cos12�㣻
��sin2(-18��)��cos248��-sin(-18��)cos48�㣻
��sin2(-25��)��cos255��-sin(-25��)cos55��.
(1)�Դ��������ʽ����ѡ��һ����������������
(2)����(1)�ļ�����������ͬѧ�ķ����ƹ�Ϊ���Ǻ��ʽ����֤����Ľ��ۣ�
��1�� ����2���������.
����2���������.
�����������������ѡ��2������sin215��+cos215��-sin15��cos15��=1- sin30��=
sin30��= ���ɵ����������ֵ��
���ɵ����������ֵ��
�����ƹ㣬�õ����Ǻ��ʽsin2��+cos2��30��-����-sin��cos��30��-����= ��
��
֤������һ��ֱ���������Dz�����ҹ�ʽ�����ʽ����ߣ�����ɵý����
֤�������������ð�ǹ�ʽ�����Dz�����ҹ�ʽ��Ҫ���ʽ�ӻ�Ϊ  ��
��
�� ������ɵý��.
������ɵý��.
�����������һ��(1)ѡ���ʽ���������£�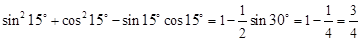 4��
4��
(2)���Ǻ��ʽΪ 6��
6��
֤�����£�


 12��
12��
������(1)ͬ��һ��
(2)���Ǻ��ʽΪ
֤�����£�



 .
.
���㣺1.���������ۺϷ���2.����������.

 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д��� ����
���� ��ʵ����ɵ�
��ʵ����ɵ� ��
�� �е����������ijһ�У���ijһ�У�����֮��Ϊ��������ı���У�����У����������ķ��ţ���Ϊһ�Ρ�������.
�е����������ijһ�У���ijһ�У�����֮��Ϊ��������ı���У�����У����������ķ��ţ���Ϊһ�Ρ�������.
(��) ���� ���1��ʾ�����������Ρ���������ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ�ʵ������д��ÿ�Ρ������������õ�������д��һ�ַ������ɣ���
���1��ʾ�����������Ρ���������ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ�ʵ������д��ÿ�Ρ������������õ�������д��һ�ַ������ɣ���
��1
| 1 | 2 | 3 |  |
 | 1 | 0 | 1 |
(��) ����
 ���2��ʾ������������һ�Ρ��������Ժ��ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ�������������
���2��ʾ������������һ�Ρ��������Ժ��ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ������������� �����п���ֵ��
�����п���ֵ����2
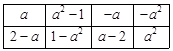
(��)����
 ��������ɵ�
��������ɵ� ��
�� �е�����һ������
�е�����һ������ ���ܷ����Ρ��������Ժ�ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ���������˵������.
���ܷ����Ρ��������Ժ�ʹ�õ�������ÿ�еĸ���֮����ÿ�еĸ���֮�;�Ϊ�Ǹ���������˵������. ��x+yi=1+2xi��x��y��R������x��y���ڣ� ��
| A��0 | B����1 | C��1 | D��2 |
���� ������
������ Ϊ������λ�����鲿�� �� ��
Ϊ������λ�����鲿�� �� ��
A�� | B�� | C�� | D�� |
 �У�
�� ����
���� �ɵȲ����У�
�ɵȲ����У� �ɵȱ�����
�ɵȱ����� .
. ��
�� .
. +
+ +��+
+��+ =
= (n��N*).
(n��N*). �ǵȲ����У�
�ǵȲ����У� ��
�� N+����
N+���� N+������Pn��Qn��һ����֤����Ľ���.
N+������Pn��Qn��һ����֤����Ľ���.