题目内容
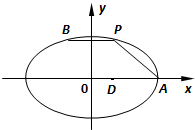 (2012•盐城一模)如图,在平面直角坐标系xoy中,已知点A为椭圆
(2012•盐城一模)如图,在平面直角坐标系xoy中,已知点A为椭圆| x2 |
| 9 |
| 2y2 |
| 9 |
| BP |
| DA |
(1)求直线BD的方程;
(2)求直线BD被过P,A,B三点的圆C截得的弦长;
(3)是否存在分别以PB,PA为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
分析:(1)根据点P,B在椭圆上,
=
,可得点B的坐标,利用两点式,我们可以求直线BD的方程;
(2)确定过P,A,B三点的圆C的圆心与半径,求出圆心到直线BD的距离,由此,我们可以得到直线BD被过P,A,B三点的圆C截得的弦长;
(3)假设存在这样的两个圆M与圆N,其中PB是圆M的弦,PA是圆N的弦,则点M一定在y轴上,点N一定在线段PC的垂直平分线y=x-1上,当圆M和圆N是两个相外切的等圆时,一定有P,M,N在一条直线上,且|PM|=|PN|,从而就可以得出结论
| BP |
| DA |
(2)确定过P,A,B三点的圆C的圆心与半径,求出圆心到直线BD的距离,由此,我们可以得到直线BD被过P,A,B三点的圆C截得的弦长;
(3)假设存在这样的两个圆M与圆N,其中PB是圆M的弦,PA是圆N的弦,则点M一定在y轴上,点N一定在线段PC的垂直平分线y=x-1上,当圆M和圆N是两个相外切的等圆时,一定有P,M,N在一条直线上,且|PM|=|PN|,从而就可以得出结论
解答:解:(1)因为
=
,且A(3,0),所以|BP|=|DA|=2,
因为
=
,及BP与x轴平行,即可得B,P关于y轴对称,
所以点P的横坐标为1,从而得P(1,2),B(-1,2)…(3分)
所以直线BD的方程为x+y-1=0…(5分)
(2)线段BP的垂直平分线方程为x=0,线段AP的垂直平分线方程为y=x-1,
所以圆C的圆心为(0,-1),且圆C的半径为r=
…(8分)
又圆心(0,-1)到直线BD的距离为d=
,
所以直线BD被圆C截得的弦长为2
=4
…(10分)
(3)假设存在这样的两个圆M与圆N,其中PB是圆M的弦,PA是圆N的弦,
则点M一定在y轴上,点N一定在线段PC的垂直平分线y=x-1上,
当圆M和圆N是两个相外切的等圆时,一定有P,M,N在一条直线上,且|PM|=|PN|…(12分)
设M(0,b),则N(2,4-b),根据N(2,4-b)在直线y=x-1上,
∴4-b=2-1,∴b=3…(14分)
所以M(0,3),N(2,1),|PM|=|PN|=
,
故存在这样的两个圆,且方程分别为x2+(y-3)2=2,(x-2)2+(y-1)2=2…(16分)
| BP |
| DA |
因为
| BP |
| DA |
所以点P的横坐标为1,从而得P(1,2),B(-1,2)…(3分)
所以直线BD的方程为x+y-1=0…(5分)
(2)线段BP的垂直平分线方程为x=0,线段AP的垂直平分线方程为y=x-1,
所以圆C的圆心为(0,-1),且圆C的半径为r=
| 10 |
又圆心(0,-1)到直线BD的距离为d=
| 2 |
所以直线BD被圆C截得的弦长为2
| r2-d2 |
| 2 |
(3)假设存在这样的两个圆M与圆N,其中PB是圆M的弦,PA是圆N的弦,
则点M一定在y轴上,点N一定在线段PC的垂直平分线y=x-1上,
当圆M和圆N是两个相外切的等圆时,一定有P,M,N在一条直线上,且|PM|=|PN|…(12分)
设M(0,b),则N(2,4-b),根据N(2,4-b)在直线y=x-1上,
∴4-b=2-1,∴b=3…(14分)
所以M(0,3),N(2,1),|PM|=|PN|=
| 2 |
故存在这样的两个圆,且方程分别为x2+(y-3)2=2,(x-2)2+(y-1)2=2…(16分)
点评:求直线方程的关键是求出点的坐标,求圆中的弦长要充分利用圆的性质,对于探究性问题,总是假设存在,再确定是否存在.

练习册系列答案
相关题目
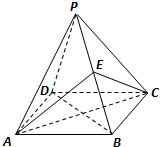 (2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.
(2012•盐城一模)如图,在四棱锥P-ABCD中,四边形ABCD是菱形,PA=PC,E为PB的中点.