题目内容
 (1)对于任意的m∈R,动直线l:(m+3)x-(m+2)y+m=0恒过一定点,求该定点坐标.
(1)对于任意的m∈R,动直线l:(m+3)x-(m+2)y+m=0恒过一定点,求该定点坐标.
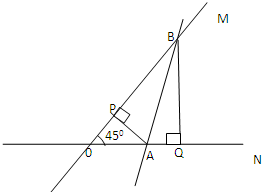
(2)两定直线ON、OM夹角θ=45°,且与动直线l分别交于点A、B,A、B在OM、ON上的射影分别为P、Q,如果直线AB过一定点,求证直线PQ也过一定点.
解:(1)对于任意的m∈R,动直线l:(m+3)x-(m+2)y+m=0转化为:m(x-y+1)+3x-2y=0,
所以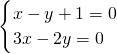 解得x=2,y=3,所以直线l:(m+3)x-(m+2)y+m=0恒过定点(2,3).
解得x=2,y=3,所以直线l:(m+3)x-(m+2)y+m=0恒过定点(2,3).
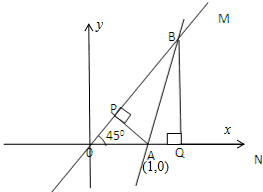
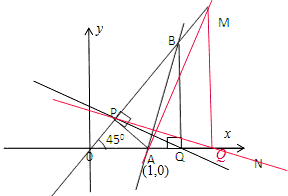
(2)建立如图所示的直角坐标系,由题意可知OM的方程为:y=x,ON的方程为:y=0,
动直线l分别交于点A、B,不妨设A为定点(1,0),直线AB的方程为:x=ny+1,(n≠1)
所以,AB与OM的交点的横坐标,由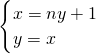 可得:x=
可得:x=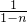 ,,(n≠1)
,,(n≠1)
即Q的坐标为(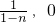 ),由题意P(
),由题意P( ),
),
所以PQ的方程为:(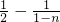 )(y-
)(y- )=
)=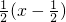 ,
,
即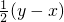 -
-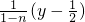 =0,因为n∈R,n≠1,
=0,因为n∈R,n≠1,
所以直线PQ恒过(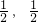 ).
).
分析:(1)按照m集项,利用任意的m∈R,方程成立,得到方程组,求出方程组的解,得到交点坐标,即可.
(2)建立直角坐标系,设出直线AB的方程,求出B、Q、P的坐标,写出PQ的方程,然后利用(1)的方法确定直线PQ也过一定点.
点评:本题是中档题,考查直线系过定点问题,注意m,n的任意性方程成立条件的应用,考查解析法证明问题的基本方法,考查计算能力.
所以
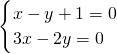 解得x=2,y=3,所以直线l:(m+3)x-(m+2)y+m=0恒过定点(2,3).
解得x=2,y=3,所以直线l:(m+3)x-(m+2)y+m=0恒过定点(2,3).(2)建立如图所示的直角坐标系,由题意可知OM的方程为:y=x,ON的方程为:y=0,
动直线l分别交于点A、B,不妨设A为定点(1,0),直线AB的方程为:x=ny+1,(n≠1)
所以,AB与OM的交点的横坐标,由
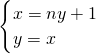 可得:x=
可得:x=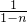 ,,(n≠1)
,,(n≠1)即Q的坐标为(
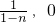 ),由题意P(
),由题意P( ),
),所以PQ的方程为:(
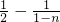 )(y-
)(y- )=
)=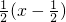 ,
,即
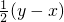 -
-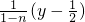 =0,因为n∈R,n≠1,
=0,因为n∈R,n≠1,所以直线PQ恒过(
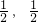 ).
).

分析:(1)按照m集项,利用任意的m∈R,方程成立,得到方程组,求出方程组的解,得到交点坐标,即可.
(2)建立直角坐标系,设出直线AB的方程,求出B、Q、P的坐标,写出PQ的方程,然后利用(1)的方法确定直线PQ也过一定点.
点评:本题是中档题,考查直线系过定点问题,注意m,n的任意性方程成立条件的应用,考查解析法证明问题的基本方法,考查计算能力.

练习册系列答案
相关题目
 (1)对于任意的m∈R,动直线l:(m+3)x-(m+2)y+m=0恒过一定点,求该定点坐标.
(1)对于任意的m∈R,动直线l:(m+3)x-(m+2)y+m=0恒过一定点,求该定点坐标.