题目内容
函数f(x)=min{2
,|x-2|},其中min{a,b}=
,若动直线y=m与函数y=f(x)的图象有三个不同的交点,它们的横坐标分别为x1,x2,x3,则x1•x2•x3的最大值为( )
| x |
|
分析:由f(x)表达式作出函数f(x)的图象,由图象可求得符合条件的m的取值范围,不妨设0<x1<x2<2<x3,通过解方程可用m把x1,x2,x3分别表示出来,利用基本不等式即可求得x1•x2•x3的最大值.
解答:解答:解:作出函数f(x)的图象如下图所示:
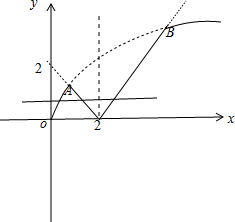 由
由
,解得A(4-2
,2
-2),
由图象可得,当直线y=m与f(x)图象有三个交点时m的范围为:0<m<2
-2.
不妨设0<x1<x2<2<x3,
则由2
=m得x1=
,由|x2-2|=2-x2=m,
得x2=2-m,由|x3-2|=x3-2=m,
得x3=m+2,且2-m>0,m+2>0,
∴x1•x2•x3=
•(2-m)•(2+m)=
•m2•(4-m2)≤
•[
]2=
×4=1,
当且仅当m2=4-m2.
即m=
时取得等号,
∴x1•x2•x3存在最大值为1.
故选A.
 由
由
|
| 3 |
| 3 |
由图象可得,当直线y=m与f(x)图象有三个交点时m的范围为:0<m<2
| 3 |
不妨设0<x1<x2<2<x3,
则由2
| x1 |
| m2 |
| 4 |
得x2=2-m,由|x3-2|=x3-2=m,
得x3=m+2,且2-m>0,m+2>0,
∴x1•x2•x3=
| m2 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| m2+4-m2 |
| 2 |
| 1 |
| 4 |
当且仅当m2=4-m2.
即m=
| 2 |
∴x1•x2•x3存在最大值为1.
故选A.
点评:点评:本题考查函数与方程的综合运用,考查基本不等式在求函数最值中的应用,考查数形结合思想,考查学生综合运用知识分析解决新问题的能力,难度较大.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目