题目内容
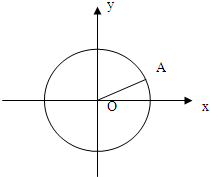 如图,设A(
如图,设A(
| ||
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
(1)求点B的坐标,并求f(t);
(2)若0≤t≤6,求
| AP |
| AB |
分析:(1)根据三角函数定义求出函数f(x)的表达式,然后求点B的坐标,并求f(t);
(2)若0≤t≤6,利用向量数量积的定义即可求
•
的取值范围.
(2)若0≤t≤6,利用向量数量积的定义即可求
| AP |
| AB |
解答:解:(1)当t=2时,∠AOB=2×
=
,
∴∠XOB=
∴,点B的坐标是(0,1)…(2分)
又t秒时,∠XOP=
+
t…(4分)
∴y=sin(
t+
),(t≥0).…(6分)
(2)由A(
,
),B(0,1),得
=(-
,
),
又P(cos(
t+
),sin(
t+
)),
∴
=(cos(
t+
)-
,sin(
t+
)-
),…(8分)
∴
•
=
-
cos(
t+
)-
+
sin(
t+
)=
+sin(
t+
-
)=
+sin(
t-
)…(10分)
∵0≤t≤6,
∴
t-
∈[-
,
],
∴sin(
t-
)∈[-
,1]…(12分)
∴,
•
的取值范围是[0,
]…(14分)
| 2π |
| 12 |
| π |
| 3 |
∴∠XOB=
| π |
| 2 |
∴,点B的坐标是(0,1)…(2分)
又t秒时,∠XOP=
| π |
| 6 |
| π |
| 6 |
∴y=sin(
| π |
| 6 |
| π |
| 6 |
(2)由A(
| ||
| 2 |
| 1 |
| 2 |
| AB |
| ||
| 2 |
| 1 |
| 2 |
又P(cos(
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∴
| AP |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴
| AP |
| AB |
| 3 |
| 4 |
| ||
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
∵0≤t≤6,
∴
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴,
| AP |
| AB |
| 3 |
| 2 |
点评:本题主要考查三角函数的定义和性质,以及平面向量的数量积运算,要求熟练掌握三角函数的图象和性质,考查学生的运算能力.

练习册系列答案
相关题目
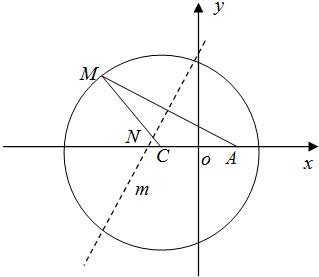 如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.
如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E. 已知椭圆E:
已知椭圆E: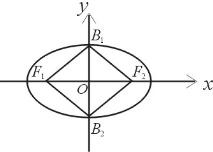 如图椭圆G:
如图椭圆G: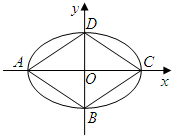 (2013•江门一模)如图,椭圆Σ:
(2013•江门一模)如图,椭圆Σ: