题目内容
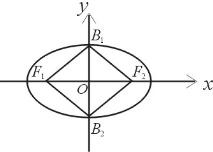 如图椭圆G:
如图椭圆G:| x2 |
| a2 |
| y2 |
| b2 |
(1)求此时椭圆G的方程;
(2)设斜率为k(k≠0)的直线l与椭圆G相交于不同的两点A、B、Q为AB的中点,且P(0,-
| ||
| 3 |
若不能,请说明理由.
分析:(1)由已知可得b=c且a2=32,可求椭圆方程
(2)设直线L的方程为y=kx+m,代入
+
=1.由直线l与椭圆相交于不同的两点可得△>0即m2<32k2+16,要使A、B两点关于过点P、Q的直线对称,必须KPQ=-
,利用方程的根与系数的关系代入得m=
,从而可求k得范围
(2)设直线L的方程为y=kx+m,代入
| x2 |
| 32 |
| y2 |
| 16 |
| 1 |
| k |
| 1+2k2 | ||
|
解答:解(1):由已知可得b=c且a2=32,
所以b2=
×32=16.∴所求椭圆方程为
+
=1.
(2)设直线L的方程为y=kx+m,代入
+
=1.
得(1+2k2)x2+4kmx+(2m2-32)=0.
由直线l与椭圆相交于不同的两点知△=(4km)2-4(1+2k2)(2m2-32)>0,
m2<32k2+16.②
要使A、B两点关于过点P、Q的直线对称,必须KPQ=-
设A(x1,y1)B(x2,y2),则xQ=
=-
,yQ=kxQ+m=
∵KPQ=
=-
解得m=
.③
由②、③得
<32k2+16
∴-
<k2<
,
∵k2>0,∴0<k2<
∴-
<k<0或0<k<
..
故当-
<k<0或0<k<
时,A、B两点关于过点P、Q的直线对称.
所以b2=
| 1 |
| 2 |
| x2 |
| 32 |
| y2 |
| 16 |
(2)设直线L的方程为y=kx+m,代入
| x2 |
| 32 |
| y2 |
| 16 |
得(1+2k2)x2+4kmx+(2m2-32)=0.
由直线l与椭圆相交于不同的两点知△=(4km)2-4(1+2k2)(2m2-32)>0,
m2<32k2+16.②
要使A、B两点关于过点P、Q的直线对称,必须KPQ=-
| 1 |
| k |
设A(x1,y1)B(x2,y2),则xQ=
| x1+x2 |
| 2 |
| 2km |
| 1+2k2 |
| m |
| 1+2k2 |
∵KPQ=
| ||||||
-
|
| 1 |
| k |
解得m=
| 1+2k2 | ||
|
由②、③得
| (1+2k2)2 |
| 3 |
∴-
| 1 |
| 2 |
| 47 |
| 2 |
∵k2>0,∴0<k2<
| 47 |
| 2 |
∴-
| ||
| 2 |
| ||
| 2 |
故当-
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了利用椭圆的性质求解椭圆的方程,直线与圆锥曲线的位置关系的综合应用,点关于直线的对称得性质的应用.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 如图,已知直线l:x=my+1过椭圆
如图,已知直线l:x=my+1过椭圆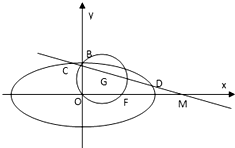 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x-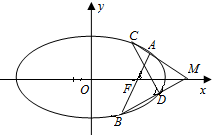 已知椭圆G:
已知椭圆G: 如图,已知椭圆G:
如图,已知椭圆G: