Question

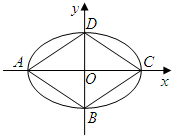（2013•江门一模）如图，椭圆Σ：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率e=

3

2

，椭圆的顶点A、B、C、D围成的菱形ABCD的面积S=4．
（1）求椭圆的方程；
（2）设直线2

2

x+y=0与椭圆Σ相交于M、N两点，在椭圆是否存在点P、Q，使四边形PMQN为菱形？若存在，求PQ的长；若不存在，简要说明理由．

Answer 1

分析：（1）利用椭圆的离心率及a，b，c的关系、菱形的面积公式即可得出；
（2）利用椭圆的对称性、线段的垂直平分线的性质、菱形的定义、两点间的距离公式．

解答：解：（1）依题意e=

c

a

=

3

2

，从而

a2-b2

a

=

3

2

，a=2b．
又S菱形=

1

2

|AC| |BD|=

1

2

×2a×2b=2ab=4，即ab=2，
联立

a=2b ab=2

，解得a=2，b=1，
∴椭圆的标准方程为

x2

4

+y2=1．
（2）存在．
由直线2

2

x+y=0可得kMN=-2

2

，
根据椭圆的对称性，当直线PQ是线段MN的垂直平分线时，PMQN为菱形，∴kPQ=-

1

kMN

=

1

2 2

，
∴PQ所在直线的方程为y=

1

2 2

x．
联立

x2 4 +y2=1 y= 1 2 2 x

解得

x= 2 6 3 y= 3 3

，

x=- 2 6 3 y=- 3 3

．
∴P(

2 6

3

，

3

3

)，Q(-

2 6

3

，-

3

3

)，
∴|PQ|=

( 2 6 3 + 2 6 3 )2+( 3 3 + 3 3 )2

=2

3

．

点评：熟练掌握椭圆的对称性、离心率及a，b，c的关系、线段的垂直平分线的性质、菱形的定义菱形的面积公式、两点间的距离公式是解题的关键．