题目内容
已知向量a=(2cos解:f(x)=a·b=![]() cos
cos![]() sin(
sin(![]() +
+![]() )+tan(
)+tan(![]() +
+![]() )tan(
)tan(![]() -
-![]() )=22cos
)=22cos![]() ·(
·(![]() sin
sin![]() +
+![]() cos
cos![]() )+
)+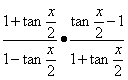
=2sin![]() cos
cos![]() +2cos2
+2cos2![]() -1
-1
=sinx+cosx
=![]() sin(x+
sin(x+![]() ).
).
所以f(x)的最大值为![]() ,最小正周期为2π,f(x)在[0,
,最小正周期为2π,f(x)在[0, ![]() ]上单调递增,在[
]上单调递增,在[![]() ,π]上单调递减.
,π]上单调递减.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知向量a=(2cos解:f(x)=a·b=![]() cos
cos![]() sin(
sin(![]() +
+![]() )+tan(
)+tan(![]() +
+![]() )tan(
)tan(![]() -
-![]() )=22cos
)=22cos![]() ·(
·(![]() sin
sin![]() +
+![]() cos
cos![]() )+
)+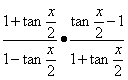
=2sin![]() cos
cos![]() +2cos2
+2cos2![]() -1
-1
=sinx+cosx
=![]() sin(x+
sin(x+![]() ).
).
所以f(x)的最大值为![]() ,最小正周期为2π,f(x)在[0,
,最小正周期为2π,f(x)在[0, ![]() ]上单调递增,在[
]上单调递增,在[![]() ,π]上单调递减.
,π]上单调递减.

 阅读快车系列答案
阅读快车系列答案