Question

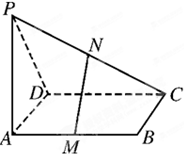如图，已知P是平行四边形ABCD所在平面外一点，M，N分别是AB，PC的中点．
（1）求证：MN∥平面PAD；
（2）若MN=BC=4，PA=4

3

，求异面直线PA与MN所成的角的大小．

Answer 1

分析：（1）取PD中点Q，连AQ、QN，根据四边形AMNQ为平行四边形可得MN∥AQ，根据直线与平面平行的判定定理可证得EF∥面PAD；
（2）根据MN∥AQ，则∠PAQ即为异面直线PA与MN所成的角，然后解三角形PAQ，可求出此角即可．

解答：（1）证明：取PD中点Q，连AQ、QN，则AM∥QN
∴四边形AMNQ为平行四边形
∴MN∥AQ
又∵AQ在平面PAD内，MN不在平面PAD内
∴MN∥面PAD；
（2）解：∵MN∥AQ
∴∠PAQ即为异面直线PA与MN所成的角
∵MN=BC=4，PA=4

3

，
∴AQ=4，根据余弦定理可知cos∠AQD+cos∠AQP=0
即

16+x2-48

8x

+

16+x2-16

8x

=0
解得x=4
在三角形AQP中，AQ=PQ=4，AP=4

3

∴cos∠PAQ=

48+16-16

2×4×4 3

=

3

2

即∠PAQ=30°
∴异面直线PA与MN所成的角的大小为30°．

点评：本题主要考查了线面平行的判定定理，以及异面直线所成角，同时考查了空间想象能力，属于基础题．