题目内容
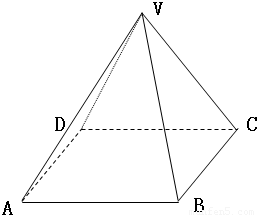
 如图,已知四棱锥V-ABCD,底面ABCD是平行四边形,点V在平面ABCD上的射影E在AD边上,且AE=
如图,已知四棱锥V-ABCD,底面ABCD是平行四边形,点V在平面ABCD上的射影E在AD边上,且AE=| 1 |
| 3 |
(Ⅰ)设F是BC的中点,求异面直线EF与VC所成角的余弦值;
(Ⅱ)设点P在棱VC上,且DP⊥EC.求
| VP |
| PC |
分析:(I)过C作CM∥FE交AD与M,连接VM,则∠VCM为异面直线EF与VC所成角,在△VCD中求CM、VC、VM的值,利用余弦定理可求异面直线所成角的余弦值;
(II)过P作PN⊥EC,交EC于N,连接DN,利用三垂线逆定理可证DN⊥EC,利用∠BCE=∠DEC=45°,求出EN、NC,利用
=
求解.
(II)过P作PN⊥EC,交EC于N,连接DN,利用三垂线逆定理可证DN⊥EC,利用∠BCE=∠DEC=45°,求出EN、NC,利用
| VP |
| PC |
| EN |
| NC |
解答:解: (Ⅰ)在平面ABCD内,过C作CM∥FE交AD与M,连接VM,
(Ⅰ)在平面ABCD内,过C作CM∥FE交AD与M,连接VM,
则∠VCM或其补角即为异面直线EF与VC所成角.
∵BE=EC=2,∠BEC=90°,∴BC=2
又四边形EFCM为平行四边形,
∴CM=EF=
BC=
,
∵VE⊥平面ABCD,CE?平面ABCD,
∴VE⊥CE,∴VC=
=2
,
∵EM=CF=
BC=
,
∴VM=
=3
,
由余弦定理得cos∠VCM=
,
故异面直线EF与VC所成角的余弦值为
.
(Ⅱ)过P作PN⊥EC,交EC于N,连接DN,
∵VE⊥平面ABCD,VE?平面VEC,
∴平面ABCD⊥平面VEC,
∴PN⊥平面ABCD,
∴DN为PD在平面ABCD内的射影
∵DP⊥EC,∴EC⊥DN.
∵∠BCE=∠DEC=45°,DE=
BC=
,
∴EN=DE×cos45°=
×
=
,NC=2-
=
,
又VE⊥平面ABCD,
故VE⊥EC,PN⊥EC,
∴PN∥VE,
故
=
=
=3.
 (Ⅰ)在平面ABCD内,过C作CM∥FE交AD与M,连接VM,
(Ⅰ)在平面ABCD内,过C作CM∥FE交AD与M,连接VM,则∠VCM或其补角即为异面直线EF与VC所成角.
∵BE=EC=2,∠BEC=90°,∴BC=2
| 2 |
又四边形EFCM为平行四边形,
∴CM=EF=
| 1 |
| 2 |
| 2 |
∵VE⊥平面ABCD,CE?平面ABCD,
∴VE⊥CE,∴VC=
| 16+4 |
| 5 |
∵EM=CF=
| 1 |
| 2 |
| 2 |
∴VM=
| 16+2 |
| 2 |
由余弦定理得cos∠VCM=
| ||
| 10 |
故异面直线EF与VC所成角的余弦值为
| ||
| 10 |
(Ⅱ)过P作PN⊥EC,交EC于N,连接DN,
∵VE⊥平面ABCD,VE?平面VEC,
∴平面ABCD⊥平面VEC,
∴PN⊥平面ABCD,
∴DN为PD在平面ABCD内的射影
∵DP⊥EC,∴EC⊥DN.
∵∠BCE=∠DEC=45°,DE=
| 3 |
| 4 |
3
| ||
| 2 |
∴EN=DE×cos45°=
3
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
又VE⊥平面ABCD,
故VE⊥EC,PN⊥EC,
∴PN∥VE,
故
| VP |
| PC |
| EN |
| NC |
| ||
|
点评:本题考查了异面直线所成的角及其求法,考查了三垂线定理的应用及线面垂直,面面垂直的性质,考查了学生的空间想象能力与推理论证能力,综合性强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
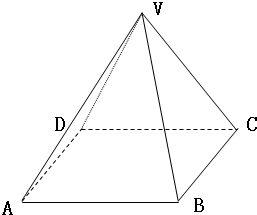 如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h. ,计算它的高和斜高.
,计算它的高和斜高.
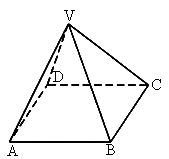
 如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.
如图,以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB;已知VA=kAB,点E是VC的中点,底面正方形ABCD边长为2a,高为h.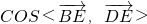 ;
;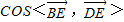 ;
;