题目内容
(14分)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为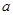 和
和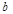 组成数对(
组成数对(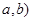 ,并构成函数
,并构成函数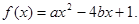
(Ⅰ)写出所有可能的数对(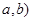 ,并计算
,并计算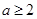 ,且
,且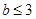 的概率;
的概率;
(Ⅱ)求函数 在区间[
在区间[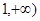 上是增函数的概率.
上是增函数的概率.
【答案】
(1)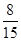 (2)
(2)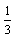
【解析】(Ⅰ)所有基本事件如下:
(1,-1),(1,1),(1,2),(1,3),(1,4),
(2,-1),(2,1),(2,2),(2,3),(2,4),
(3,-1),(3,1),(3,2),(3,3),(3,4) ,共有15个。………………………………4分
设事件“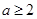 ,且
,且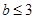 ”为A,
”为A,
则事件A包含的基本事件有8个, ………………………………… 6分
所以P(A)=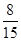 。
……………………………………………8分
。
……………………………………………8分
(Ⅱ)设事件“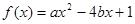 在区间
在区间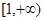 上为增函数”为B,
上为增函数”为B,
因函数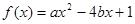 的图象的对称轴为
的图象的对称轴为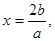 且
且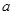 >0,
>0,
所以要使事件B发生,只需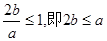 。…………………………10分
。…………………………10分
由满足题意的数对有(1,-1)、(2,-1)、(2,1)、(3,-1)、(3,1),共5个,
…………………………12分
所以,P(B)= 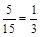 .
…………………………14分
.
…………………………14分

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目