题目内容
设集合P={1,2,3,4,5,6,7,8},P的子集A={a1,a2,a3},其中a3>a2>a1,当满足a3≥a2+2≥a1+5时,我们称子集A为P的“好子集”,则这种“好子集”的个数为
10
10
.(用数字作答)分析:通过新定义,可知a2-a1≥3,a3-a2≥2,可以一一列举满足题意的集合即可.
解答:解:由题意可知a2-a1≥3,a3-a2≥2,满足题意的集合如图:
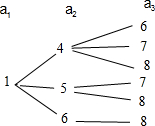 ,
,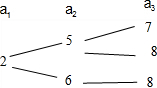 ,
,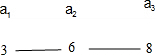
这样的集合有10个.
故答案为:10.
 ,
, ,
,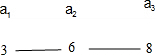
这样的集合有10个.
故答案为:10.
点评:本题是中档题,考查新定义的理解与应用,列举法是解题的基本方法,这样题目中三个元素的关系是解题的关键.

练习册系列答案
相关题目