题目内容
(12分)将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为6的概率;
(2)两数之积是6的倍数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率。
(1)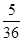 ;(2)
;(2)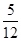 ;(3)
;(3)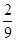 ;
;
解析试题分析:(1)先后抛掷2次骰子,每次出现1,2,3,4,5,6点的概率都是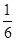 ,两数之和的情况有
,两数之和的情况有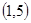 ,
,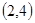 ,
,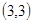 ,
,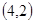 ,
,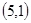 ;共5钟情况,所以概率为
;共5钟情况,所以概率为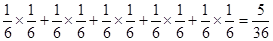 。(2)两数之积是6的倍数的有6,12,18,24,30,36;积为6的情况有
。(2)两数之积是6的倍数的有6,12,18,24,30,36;积为6的情况有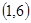 ,
,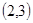 ,
,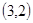 ,
,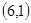 两种概率为
两种概率为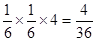 ,积为12的情况有
,积为12的情况有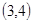 ,
,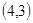 ,
,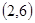 ,
, 两种概率为
两种概率为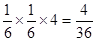 ,积为18的情况有
,积为18的情况有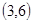 ,
,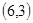 两种概率为
两种概率为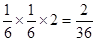 ,积为24的情况有
,积为24的情况有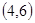 ,
,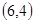 两种
两种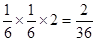 ,积为30的情况有
,积为30的情况有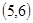 ,
,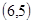 两种概率为
两种概率为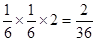 ,积为36的情况有
,积为36的情况有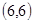 一种概率为
一种概率为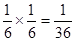 ,所以两数之积是6的倍数的概率为
,所以两数之积是6的倍数的概率为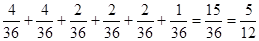 。(3)在圆
。(3)在圆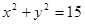 的内部,即要满足
的内部,即要满足 ,所以有当
,所以有当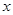 取1,
取1,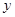 对应可取1,2,3;当
对应可取1,2,3;当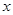 取2,
取2,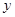 对应可取1,2,3;当
对应可取1,2,3;当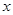 取3,
取3,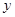 对应可取1,2;所以概率为
对应可取1,2;所以概率为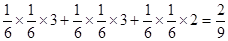 。
。
试题解析:解:(1)两数之和为6的概率为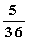 。
。
(2)此问题中含有36个等可能基本事件,记“向上的两数之积是6的倍数”为事件A,则由下面的列表可知,事件A中含有其中的15个等可能基本事件,所以P(A)= 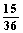 =
=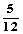 ,
,
所以两数之积是6的倍数的概率为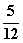 。
。
此问题共含36个等可能基本事件,而点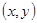 在圆
在圆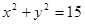 的内部有
的内部有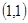 ,
,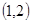 ,
,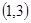 ,
,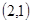 ,
,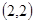 ,
,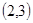 ,
,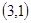 ,
,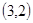 共8种,所以概率为
共8种,所以概率为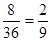 。
。
考点:古典概型

 阅读快车系列答案
阅读快车系列答案某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: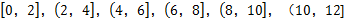 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.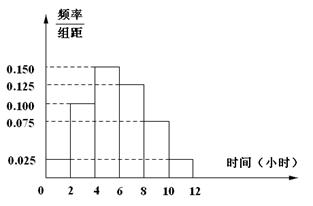
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有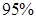 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附: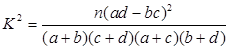
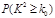 | 0.10 | 0.05 | 0.010 | 0.005 |
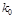 | 2.706 | 3.841 | 6.635 | 7.879 |
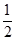 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: 的分别列与期望E
的分别列与期望E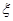 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的概率分布及数学期望.
的概率分布及数学期望.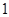 个、黄色球
个、黄色球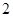 个、蓝色球
个、蓝色球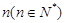 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得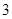 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出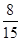 .
.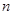 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出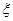 表示所摸
表示所摸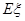 .
.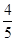 ,
,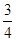 ,
, ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.