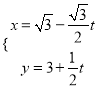题目内容
【题目】已知向量a=(sin x,mcos x),b=(3,-1).
(1)若a∥b,且m=1,求2sin2x-3cos2x的值;
(2)若函数f(x)=a·b的图象关于直线![]() 对称,求函数f(2x)在
对称,求函数f(2x)在![]() 上的值域.
上的值域.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:
(1)由题意![]() ,可求解
,可求解![]() ,再根据
,再根据![]()
![]() ,即可求解
,即可求解![]() 在
在![]() 的值域.
的值域.
(2)由![]() ,关于
,关于![]() 对称,求得
对称,求得![]() ,进而得到函数
,进而得到函数![]() 的解析式,即可求解函数
的解析式,即可求解函数
试题解析:
(1)当m=1时,a=(sin x,cos x),又b=(3,-1),
且a∥b.
∴-sin x-3cos x=0,即tan x=-3,
∵2sin2x-3cos2x=![]() =
=![]() =
=![]() =
=![]() ,
,
∴2sin2x-3cos2x=![]() .
.
(2)∵f(x)=a·b=3sin x-mcos x的图象关于直线
x=![]() 对称,
对称,
∴f![]() =f
=f![]() ,即f
,即f![]() =f
=f![]() ,
,
即3=![]() +
+![]() m,得m=
m,得m=![]() ,
,
则f(x)=2![]()
![]() =2
=2![]() sin
sin![]() ,
,
∴f(2x)=2![]() sin
sin![]() ,
,
∵x∈![]() ,∴2x-
,∴2x-![]() ∈
∈![]() ,
,
∴当x=![]() 时,f(2x)取最大值为2
时,f(2x)取最大值为2![]() ;当x=
;当x=![]() 时,f(2x)取最小值为-
时,f(2x)取最小值为-![]() .
.
即函数f(2x)在![]() 上的值域为[-
上的值域为[-![]() ,2
,2![]() ].
].

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目