题目内容
(2009四川卷文)设数列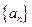 的前
的前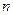 项和为
项和为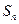 ,对任意的正整数
,对任意的正整数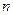 ,都有
,都有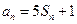 成立,记
成立,记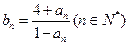 。
。
(I)求数列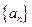 与数列
与数列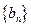 的通项公式;
的通项公式;
(II)设数列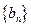 的前
的前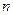 项和为
项和为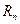 ,是否存在正整数
,是否存在正整数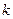 ,使得
,使得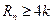 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数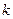 ;若不存在,请说明理由;
;若不存在,请说明理由;
(III)记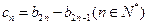 ,设数列
,设数列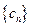 的前
的前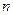 项和为
项和为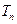 ,求证:对任意正整数
,求证:对任意正整数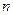 都有
都有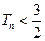 ;
;
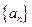 的前
的前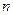 项和为
项和为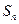 ,对任意的正整数
,对任意的正整数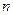 ,都有
,都有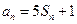 成立,记
成立,记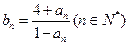 。
。 (I)求数列
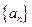 与数列
与数列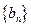 的通项公式;
的通项公式;(II)设数列
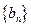 的前
的前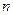 项和为
项和为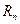 ,是否存在正整数
,是否存在正整数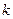 ,使得
,使得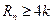 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数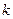 ;若不存在,请说明理由;
;若不存在,请说明理由;(III)记
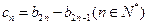 ,设数列
,设数列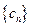 的前
的前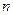 项和为
项和为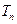 ,求证:对任意正整数
,求证:对任意正整数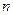 都有
都有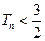 ;
;解(I)当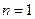 时,
时,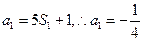
又
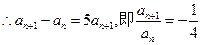
∴数列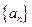 是首项为
是首项为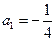 ,公比为
,公比为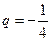 的等比数列,
的等比数列,
∴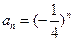 ,
,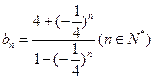 …………………………………3分
…………………………………3分
(II)不存在正整数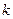 ,使得
,使得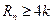 成立。
成立。
证明:由(I)知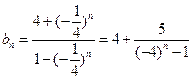
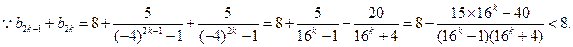
∴当n为偶数时,设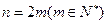
∴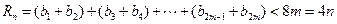
当n为奇数时,设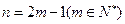
∴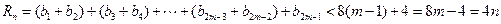
∴对于一切的正整数n,都有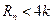
∴不存在正整数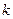 ,使得
,使得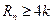 成立。 …………………………………8分
成立。 …………………………………8分
(III)由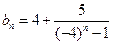 得
得
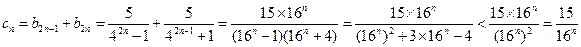 又
又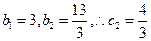 ,
,
当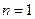 时,
时,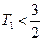 ,
,
当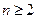 时,
时,
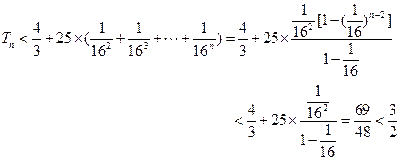
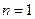 时,
时,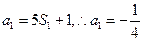
又

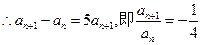
∴数列
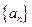 是首项为
是首项为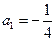 ,公比为
,公比为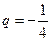 的等比数列,
的等比数列,∴
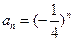 ,
,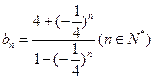 …………………………………3分
…………………………………3分(II)不存在正整数
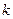 ,使得
,使得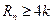 成立。
成立。证明:由(I)知
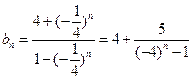
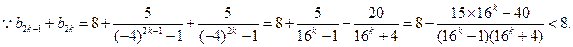
∴当n为偶数时,设
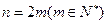
∴
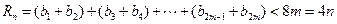
当n为奇数时,设
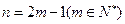
∴
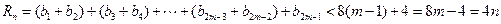
∴对于一切的正整数n,都有
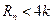
∴不存在正整数
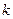 ,使得
,使得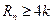 成立。 …………………………………8分
成立。 …………………………………8分(III)由
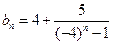 得
得 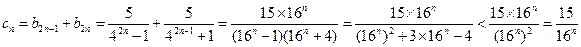 又
又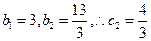 ,
, 当
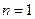 时,
时,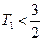 ,
,当
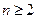 时,
时,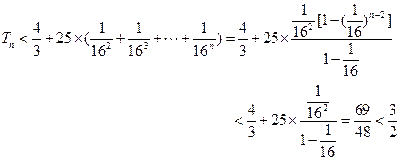
略

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
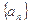 的前n项和为
的前n项和为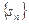 ,且
,且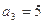 ,
,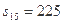
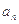
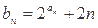 ,求数列
,求数列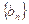 的前n项和
的前n项和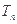
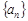 中,
中,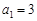 ,
,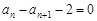 ,则
,则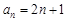
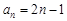
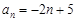
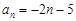
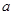 ,第三年的增长率为
,第三年的增长率为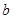 ,则这两年的年平均增长率记为
,则这两年的年平均增长率记为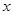 ,则( )
,则( )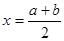
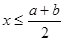
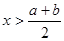
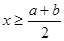

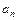 =1+
=1+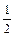 +
+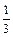 +…+
+…+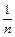 (n
(n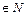 ),
),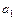 +
+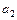 +…+
+…+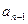 =g(n)(
=g(n)(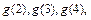 并猜想
并猜想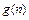 的表达式;
的表达式;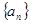 中,
中,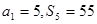 ,则公比
,则公比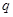 等于 ( )
等于 ( )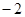
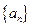 是等差数列,且
是等差数列,且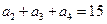 ,则这个数列的前5项和
,则这个数列的前5项和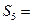 ( )
( )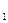 =1,a
=1,a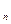 =a
=a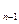 +3(n≥2,n∈N
+3(n≥2,n∈N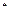 ),则a
),则a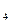 ="( " )
="( " )