题目内容
设函数f（x）定义在实数集上，当x≥1时，f（x）=3x-1，且f（x+1）是偶函数，则有（ ）A．
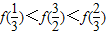
B．
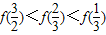
C．
D．
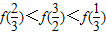
【答案】分析：当x≥1时，f（x）=3x-1，单调递增，利用f（x+1）是偶函数把f（
）、f（
）转化为区间[1，+∞）上的函数值即可比较大小．
解答：解：因为f（x+1）是偶函数，所以f（x+1）=f（1-x），
所以f（
）=f（1-
）=f（1+
）=f（
），f（
）=f（1-
）=f（1+
）=f（
），
又当x≥1时，f（x）=3x-1，单调递增，
＜
＜
，所以f（
）＜f（
）＜f（
），
即f（
）＜f（
）＜f（
）．
故选D．
点评：本题考查了函数的单调性及其应用，解决本题的关键是对f（
）、f（
）进行转化，然后利用函数f（x）在[1，+∞）上的单调性解决．
）、f（）转化为区间[1，+∞）上的函数值即可比较大小．解答：解：因为f（x+1）是偶函数，所以f（x+1）=f（1-x），
所以f（
）=f（1-）=f（1+）=f（），f（）=f（1-）=f（1+）=f（），又当x≥1时，f（x）=3x-1，单调递增，
＜＜，所以f（）＜f（）＜f（），即f（
）＜f（）＜f（）．故选D．
点评：本题考查了函数的单调性及其应用，解决本题的关键是对f（
）、f（）进行转化，然后利用函数f（x）在[1，+∞）上的单调性解决． 
练习册系列答案
阅读快车系列答案
相关题目