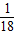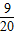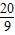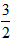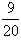Question

若随机变量ξ的分布列如下表，且a，b，c，d组成以a为首项，

1

2

为公比的等比数列，则Eξ的值为

26

15

	1	2	3	4
P	a	b	c	d

Answer 1

分析：先根据a，b，c，d组成以a为首项，

1

2

为公比的等比数列，以及所求概率和为1建立等式，求出a的值，最后根据数学期望公式解之即可．

解答：解：∵a，b，c，d组成以a为首项，

1

2

为公比的等比数列
∴b=

1

2

a，c=

1

4

a，d=

1

8

a，
根据概率和为1则a+

1

2

a+

1

4

a+

1

8

a=1，解得a=

8

15

∴Eξ=a+2b+3c+4d=a+a+

3

4

a+

1

2

a=

13

4

a=

26

15

故答案为：

26

15

点评：本题主要考查了离散型随机变量的期望，以及所求概率和为1和等比数列的求和，属于中档题．