题目内容
作出下列函数的图象(1)y=sinx|cosx|+cosx|sinx|;
(2)y=
| ||
|
分析:(1)易求得函数的周期为2π,函数中含有绝对值,故可去绝对值,分x∈[0,
],[
,π],[π,
π],[
π,2π]四段去绝对值,转化为简单函数作图即可.
(2)1+cos2x=2cos2x,由cosx的符号分段讨论,转化为与tanx有关的函数,画出图象即可.
| π |
| 2 |
| π |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(2)1+cos2x=2cos2x,由cosx的符号分段讨论,转化为与tanx有关的函数,画出图象即可.
解答:解:(1)易求得函数的周期为2π,可作出函数在[0,2π]上的图象,再两边平移2kπ个单位即可.
y=sinx|cosx|+cosx|sinx|=
如图: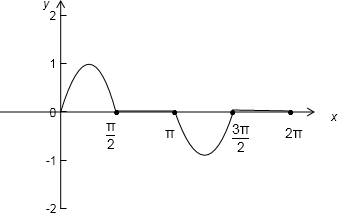
(2)y=
=
=
=
如图所示: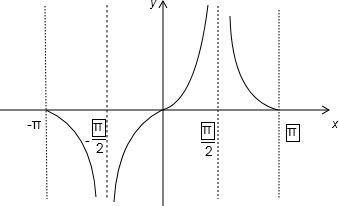
y=sinx|cosx|+cosx|sinx|=
|
如图:

(2)y=
| ||
|
| ||
|
| sinx |
| |cosx| |
|
如图所示:

点评:本题考查三角函数的化简、三角函数作图,考查作图能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目