题目内容
【题目】已知椭圆![]() (a>b>0)的左右焦点分别为F1,F2,图象经过点A(2,0)和点B(0,
(a>b>0)的左右焦点分别为F1,F2,图象经过点A(2,0)和点B(0,![]() )过F2与坐标轴不垂直的直线l与椭圆C交于P,Q两点,N为PQ的中点.
)过F2与坐标轴不垂直的直线l与椭圆C交于P,Q两点,N为PQ的中点.
(1)求椭圆C的方程;
(2)设点![]() ,且MN⊥PQ于N,求直线PQ的方程.
,且MN⊥PQ于N,求直线PQ的方程.
【答案】(1)![]() (2)直线PQ的方程为y
(2)直线PQ的方程为y![]() (x﹣1),或y
(x﹣1),或y![]() (x﹣1)
(x﹣1)
【解析】
(1)由图象经过点![]() 和点
和点![]() ,可得
,可得![]() ,
,![]() ,即得椭圆
,即得椭圆![]() 的方程;
的方程;
(2)因为直线![]() 的斜率存在,设直线方程为
的斜率存在,设直线方程为![]() ,P(x1,y1),Q(x2,y2),联立直线方程与椭圆方程,由韦达定理求解出
,P(x1,y1),Q(x2,y2),联立直线方程与椭圆方程,由韦达定理求解出![]() 的坐标,根据
的坐标,根据![]() ,转化求解即可.
,转化求解即可.
(1)∵图象经过点A(2,0)和点B(0,![]() ),
),
∴a=2,b![]() , ∴椭圆C的方程为
, ∴椭圆C的方程为![]() 1;
1;
(2)因为直线PQ的斜率存在,设直线方程为y=k(x﹣1),P(x1,y1),Q(x2,y2),
联立 整理得(3+4k2)x2﹣8k2x+4k2﹣12=0,
整理得(3+4k2)x2﹣8k2x+4k2﹣12=0,
由韦达定理知x1+x2![]() ,y1+y2=k(x1+x2)﹣2k
,y1+y2=k(x1+x2)﹣2k![]()
此时N(![]() ,
,![]() ),又M(0,
),又M(0,![]() ),则kMN
),则kMN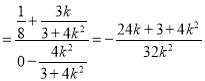 ,
,
∵MN⊥PQ,∴kMN![]() ,解得k
,解得k![]() 或k
或k![]() .
.
∴直线PQ的方程为y![]() (x﹣1),或y
(x﹣1),或y![]() (x﹣1).
(x﹣1).

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目