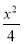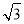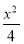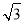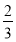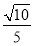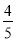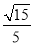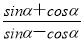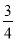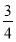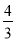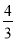题目内容
已知椭圆中心在坐标原点,焦点在x轴上,离心率为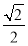 ,它的一个顶点为抛物线x2=4y的焦点.
,它的一个顶点为抛物线x2=4y的焦点.
(1)求椭圆方程;
(2)若直线y=x-1与抛物线相切于点A,求以A为圆心且与抛物线的准线相切的圆的方程;
(3)若斜率为1的直线交椭圆于M、N两点,求△OMN面积的最大值(O为坐标原点).
(1)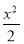 +y2=1(2)(x-2)2+(y-1)2=4(3)
+y2=1(2)(x-2)2+(y-1)2=4(3) 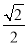
【解析】(1)由题意设椭圆方程为: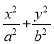 =1(a>b>0),
=1(a>b>0),
因为抛物线x2=4y的焦点为(0,1),
所以b=1.由离心率e=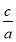 =
=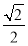 ,a2=b2+c2解得a=
,a2=b2+c2解得a=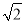 ,b=1,c=1,椭圆方程为
,b=1,c=1,椭圆方程为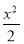 +y2=1.
+y2=1.
(2)由 解得
解得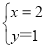 ,所以A=(2,1).
,所以A=(2,1).
因为抛物线的准线方程为y=-1,
所以圆的半径r=1-(-1)=2,
所以圆的方程为(x-2)2+(y-1)2=4.
(3)设直线MN方程为y=x+m,由 得3x2+4mx+2m2-2=0.
得3x2+4mx+2m2-2=0.
由判别式Δ=16m2-12(2m2-2)>0,解得-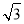 <m<
<m<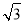 .
.
设M(x1,y1),N(x2,y2),则x1+x2=-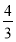 m,x1x2=
m,x1x2=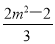 ,
,
所以|MN|=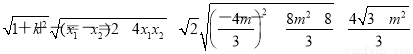
原点O到直线MN的距离d=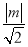
S=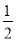 |MN|d=
|MN|d=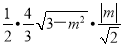 =
=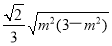 ≤
≤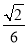 (m2+3-m2)=
(m2+3-m2)=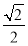 .
.
当且仅当m2=3-m2即m=±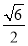 时等号成立,所以三角形OMN面积的最大值为
时等号成立,所以三角形OMN面积的最大值为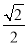 .
.

练习册系列答案
相关题目
已知x,y取值如下表:
x | 0 | 1 | 4 | 5 | 6 | 8 |
y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
从所得的散点图分析可知:y与x线性相关,且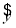 =0.95x+a,则a=( ).
=0.95x+a,则a=( ).
A.1.30 B.1.45 C.1.65 D.1.80