题目内容

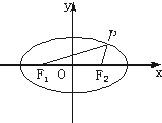精英家教网P是以F1、F2为焦点的椭圆上一点，且∠PF1F2=α，∠PF2F1=2α，求证：椭圆的离心率为e=2cosα-1．
分析：依据椭圆的定义2a=|PF1|+|PF2|，2c=|F1F2|，又由e=
2c
2a
，在△PF1F2中解此三角即可得证．
解答：证明：在△PF1F2中，由正弦定理知
|PF1|
sin2α
=
|PF2|
sinα
=
|F1F2|
sin(π-3α)
．
由比例的性质得
|F1F2|
sin3α
=
|PF1|+|PF2|
sin2α+sinα
?e=
|F1F2|
|PF1|+|PF2|
=
sin3α
sin2α+sinα
=
sinαcos2α+cosαsin2α
sinα+2sinαcos α

=
sinα(2cos2α-1)+2sinα•cos2α
sin(1+2cosα)

=
4cos2α-1
2cosα+1
=2cosα-1．
点评：本题主要考查了椭圆的应用．恰当地利用比例的性质有事半功倍之效．
练习册系列答案
相关题目
设P是以F1、F2为焦点的椭圆
x2
b2
+
y2
a2
=1 (a＞b＞0)上的任一点，∠F1PF2最大值是120°，求椭圆离心率．
已知P是以F1，F2为焦点的椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上的一点，若PF1⊥PF2，tan∠PF1F2=
1
2
，则此椭圆的离心率为（　　）
A、
1
2
B、
2
3
C、
1
3
D、
5
3
已知P是以F1，F2为焦点的双曲线
x2
a2
-
y2
b2
=1上的一点，若
PF1
•
PF2
=0，tan∠PF1F2=2，则此双曲线的离心率为（　　）
A、
5
B、5
C、2
5
D、3
若P是以F1，F2为焦点的椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)上的一点，且
PF1
•
PF2
=0，tan∠PF1F2=
1
2
，则此椭圆的离心率为（　　）
已知点P是以F1，F2为焦点的椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)上一点，且
PF1
•
PF2
=0，tan∠PF1F2=
1
2
，则该椭圆的离心率等于
5
3
5
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网