题目内容
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为 ,乙队每人答对的概率都是
,乙队每人答对的概率都是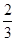 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用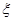 表示甲队总得分.
表示甲队总得分.
(I)求随机变量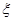 的分布列及其数学期望E(
的分布列及其数学期望E(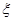 );
);
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
(I)如下(Ⅱ)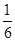
解析试题分析:解:(1)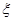 的可能取值为0,1,2,3
的可能取值为0,1,2,3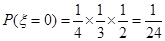 ;
;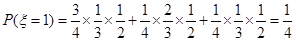 ;
;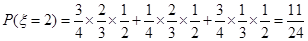 ;
;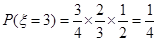
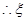 的分布列为
的分布列为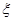
0 1 2 3 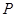
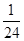
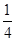
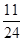
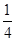
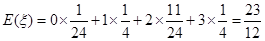
(2)设“甲队和乙队得分之和为4”为事件A,“甲队比乙队得分高”为事件B
则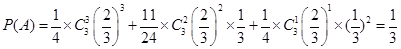 ;
;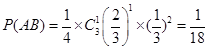
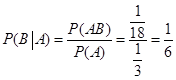
考点:分布列及其数学期望;概率
点评:求随机变量的分布列和数学期望是常考题型,解决这种题目关键是求出随机变量对应的概率。

练习册系列答案
相关题目
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表:
| 日销售量(吨) | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
(2)若以频率为概率,且每天的销售量相互独立.
①求5天中该种商品恰有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2万元,X表示该种商品两天销售利润的和,求X的分布列和数学期望.
 ,
, ,
,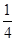 ,
,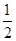 .游戏规则如下:
.游戏规则如下: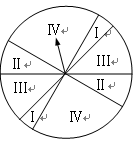
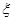 .
.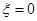 的概率;
的概率;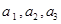 ,女生2名,记为
,女生2名,记为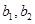 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛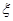 的概率密度函数
的概率密度函数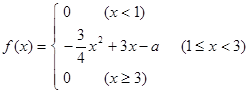 ,
, 的值,并画出
的值,并画出
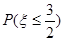 .
.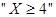 的概率。
的概率。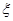 ,求
,求
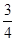 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有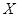 名获得优秀,求
名获得优秀,求