题目内容
已知球的表面积为20π,球面上有A、B、C三点,如果AB=AC=2,BC=A.1 B.![]() C.
C.![]() D.2
D.2
解析:球的表面积为20π,即S=4πR2=20π,∴R=![]() .
.

在△ABC中,AB=AC=2,BC=![]() ,
,
∴由余弦定理得cosA=![]() .
.
∴A=120°.
设△ABC外接圆的半径为r,则由正弦定理得![]() =2r,
=2r,
∴r=2.∴所求距离d=![]() =1.
=1.
答案:A

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
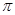 ,球面上有A、B、C三点,如果AB=AC=2,BC=2
,球面上有A、B、C三点,如果AB=AC=2,BC=2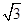 ,则球心到平面ABC的距离为( )
,则球心到平面ABC的距离为( )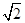 C.
C.