题目内容
(2012•武汉模拟)已知圆M:x2+y2-8x-6y=0,过圆M内定点P(1,2)作两条相互垂直的弦AC和BD,则四边形ABCD面积的最大值为( )
分析:设圆心到AC、BD的距离分别为d1、d2,则 d12+d22=8,代入面积公式S=
×AC×BD,使用基本不等式求出四边形ABCD的面积的最大值.
| 1 |
| 2 |
解答: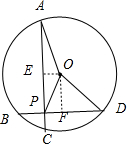 解:圆M:x2+y2-8x-6y=0,
解:圆M:x2+y2-8x-6y=0,
即:(x-4)2+(y-3)2=25
设圆心T(O)到AC、BD的距离分别为d1、d2,则d12+d22=TP2=OP2=8..
四边形ABCD的面积为:
S=
×|AB|×|CD|=
×2
=2
×
≤50-(d12+d22)=42.
当且仅当d12=d22时取等号,
故选 D.
 解:圆M:x2+y2-8x-6y=0,
解:圆M:x2+y2-8x-6y=0,即:(x-4)2+(y-3)2=25
设圆心T(O)到AC、BD的距离分别为d1、d2,则d12+d22=TP2=OP2=8..
四边形ABCD的面积为:
S=
| 1 |
| 2 |
| 1 |
| 2 |
=2
| 25 -d12 |
| 25-d 22 |
当且仅当d12=d22时取等号,
故选 D.
点评:此题考查学生掌握垂径定理及勾股定理的应用,灵活运用两点间的距离公式化简求值,是一道中档题.学生做题时注意对角线垂直的四边形的面积等于对角线乘积的一半.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 (2012•武汉模拟)如图是一正方体被过棱的中点M、N,顶点A和N、顶点D、C1的两上截面截去两个角后所得的几何体,则该几何体的正视图为( )
(2012•武汉模拟)如图是一正方体被过棱的中点M、N,顶点A和N、顶点D、C1的两上截面截去两个角后所得的几何体,则该几何体的正视图为( )