题目内容

（2012•武汉模拟）F1、F2是双曲线
x2
16
-
y2
20
=1的焦点，点P在双曲线上，若点P到焦点F1的距离等于9，则点P到焦点F2的距离等于
17
17
．
分析：根据双曲线的定义||PF1|-|PF2||=2a=12，已知|PF1|=9，进而可求|PF2|．
解答：解：∵双曲线
x2
16
-
y2
20
=1得：a=4，
由双曲线的定义知||PF1|-|PF2||=2a=8，|PF1|=9，
∴|PF2|=1＜（不合，舍去）或|PF2|=17，
故|PF2|=17．
故答案为17．
点评：本题主要考查了双曲线的性质，运用双曲线的定义||PF1|-|PF2||=2a，是解题的关键，属基础题．
练习册系列答案
相关题目
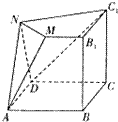（2012•武汉模拟）如图是一正方体被过棱的中点M、N，顶点A和N、顶点D、C1的两上截面截去两个角后所得的几何体，则该几何体的正视图为（　　）
（2012•武汉模拟）天气预报说，在今后的三天中，每一天下雨的概率均为40%．现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率：先利用计算器产生0到9之间取整数值的随机数，用1，2，3，4表示下雨，用5，6，7，8，9，0表示不下雨；再以每三个随机数作为一组，代表这三天的下雨情况．经随机模拟试验产生了如下20组随机数：
907    966    191    925    271    932    812    458    569    683
431    257    393    027    556    488    730    113    537    989
据此估计，这三天中恰有两天下雨的概率近似为（　　）
（2012•武汉模拟）已知函数f(x)=
lnx
x
-1．
（1）求函数f（x）的单调区间；
（2）设m＞0，求函数f（x）在[m，2m]上的最大值；
（3）证明：对?n∈N*，不等式ln(
2+n
n
)＜
2+n
n
恒成立．
（2012•武汉模拟）若复数z满足（2-i）z=1+i（i为虚数单位），则复数z在复平面内对应的点的坐标为
（
1
5
，
3
5
）
（
1
5
，
3
5
）
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网