题目内容
某运动员训练次数与训练成绩之间的数据关系如下:
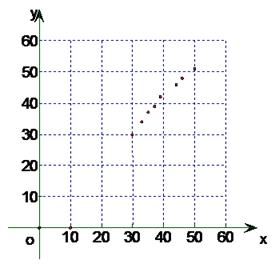
⑴在图1坐标系中做出散点图;
⑵求出回归方程;
⑶计算相关系数,并利用其检验两个变量的相关关系的显著性;
⑷在图2中做出残差图;
⑸计算相关指数 ;
;
⑹试预测该运动员训练47次及55次的成绩.


| 次数(x) | 30 | 33 | 35 | 37 | 39 | 44 | 46 | 50 |
| 成绩(y) | 30 | 34 | 37 | 39 | 42 | 46 | 48 | 51 |
⑵求出回归方程;
⑶计算相关系数,并利用其检验两个变量的相关关系的显著性;
⑷在图2中做出残差图;
⑸计算相关指数
 ;
;⑹试预测该运动员训练47次及55次的成绩.


略
⑴做出该运动员训练次数x和与成绩y的散点图,如果所示,由散点图可知,它们之间具有相关关系.
列表计算如右图所示:
由表可知,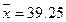 ,
, ,
,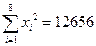 ,
,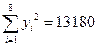 ,
,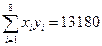 ,
,
所以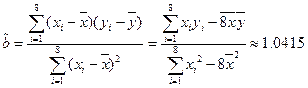 ,
,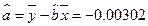 ,
,
所以回归直线方程为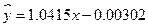 .
.
⑶计算相关系数:讲上面的数据代入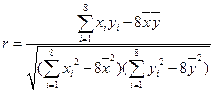 ,得
,得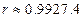 ,显然
,显然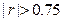 ,故
,故 与
与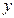 具有很强的相关关系.
具有很强的相关关系.
⑷残差分析:下面的表格列出了运动员训练次数和成绩的原始数据以及相应的残差数据.
做残差图,如图所示,由图可知,残差点比较均匀地分布在水平带状区域内,说明选择的模型比较合适.
⑸计算相关指数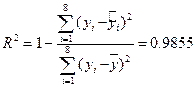 ,说明了该运动员的成绩的差异有98.55%是由训练次数引起的.
,说明了该运动员的成绩的差异有98.55%是由训练次数引起的.
⑹做出预报:由上述分析可知,回归直线方程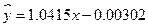 可以作为该运动员训练成绩的预报值.
可以作为该运动员训练成绩的预报值.
将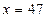 和
和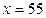 分别代入该方程可得
分别代入该方程可得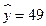 、
、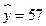 ,故预测该运动员训练47次和55次的成绩分别为49和55.
,故预测该运动员训练47次和55次的成绩分别为49和55.

列表计算如右图所示:
次数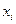 | 成绩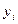 | 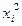 | 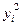 | 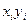 |
| 30 | 30 | 900 | 900 | 900 |
| 33 | 34 | 1089 | 1156 | 1122 |
| 35 | 37 | 1225 | 1369 | 1295 |
| 37 | 39 | 1369 | 1521 | 1443 |
| 39 | 42 | 1521 | 1764 | 1638 |
| 44 | 46 | 1936 | 2116 | 2024 |
| 46 | 48 | 2116 | 2304 | 2208 |
| 50 | 51 | 2500 | 2601 | 2550 |
由表可知,
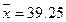 ,
, ,
,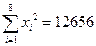 ,
,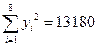 ,
,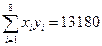 ,
,所以
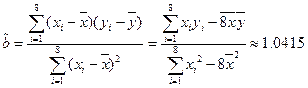 ,
,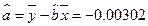 ,
,所以回归直线方程为
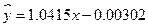 .
.⑶计算相关系数:讲上面的数据代入
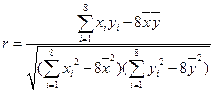 ,得
,得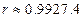 ,显然
,显然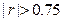 ,故
,故 与
与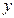 具有很强的相关关系.
具有很强的相关关系.⑷残差分析:下面的表格列出了运动员训练次数和成绩的原始数据以及相应的残差数据.
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
次数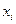 | 30 | 33 | 35 | 37 | 39 | 44 | 46 | 50 |
成绩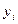 | 30 | 34 | 37 | 39 | 42 | 46 | 48 | 51 |
预报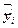 | 31.24198 | 34.36648 | 36.44948 | 38.53248 | 40.61548 | 45.82298 | 47.90598 | 52.07198 |
残差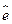 | -1.24198 | -0.36648 | 0.55052 | 0.46752 | 1.38452 | 0.17702 | 0.09402 | -1.07198 |

⑸计算相关指数
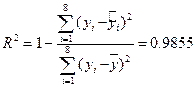 ,说明了该运动员的成绩的差异有98.55%是由训练次数引起的.
,说明了该运动员的成绩的差异有98.55%是由训练次数引起的.⑹做出预报:由上述分析可知,回归直线方程
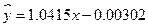 可以作为该运动员训练成绩的预报值.
可以作为该运动员训练成绩的预报值.将
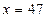 和
和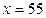 分别代入该方程可得
分别代入该方程可得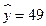 、
、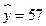 ,故预测该运动员训练47次和55次的成绩分别为49和55.
,故预测该运动员训练47次和55次的成绩分别为49和55.
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 语文
语文 的观测值
的观测值 问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?
问在多大程度上可以认为高中生的语文与数学成绩之间有关系?为什么?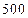 名患者身上试验某种血清治疗
名患者身上试验某种血清治疗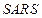 的作用,与另外
的作用,与另外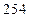
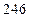
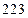
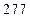
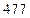
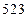
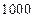
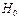 条件下的小概率事件,若在一次试验中该事件发生了,这是与实际推断相抵触的“不合理”现象,则作出拒绝
条件下的小概率事件,若在一次试验中该事件发生了,这是与实际推断相抵触的“不合理”现象,则作出拒绝