题目内容
【题目】数列![]() 满足
满足![]() .
.
①存在![]() 可以生成的数列
可以生成的数列![]() 是常数数列;
是常数数列;
②“数列![]() 中存在某一项
中存在某一项![]() ”是“数列
”是“数列![]() 为有穷数列”的充要条件;
为有穷数列”的充要条件;
③若![]() 为单调递增数列,则
为单调递增数列,则![]() 的取值范围是
的取值范围是![]() ;
;
④只要![]() ,其中
,其中![]() ,则
,则![]() 一定存在;
一定存在;
其中正确命题的序号为__________.
【答案】①④
【解析】
根据已知中数列![]() 满足
满足![]() .举出正例
.举出正例![]() 或
或![]() ,可判断①;举出反例
,可判断①;举出反例![]() ,可判断②;举出反例
,可判断②;举出反例![]() ,可判断③;构造数列
,可判断③;构造数列![]() ,结合已知可证得数列
,结合已知可证得数列![]() 是以
是以![]() 为公比的等比数列,进而可判断④.
为公比的等比数列,进而可判断④.
解:当![]() 时,
时,![]() 恒成立,当
恒成立,当![]() 时,
时,![]() 恒成立,故①正确;
恒成立,故①正确;
当![]() 时,则
时,则![]() ,由递推公式
,由递推公式![]() ,可知数列
,可知数列![]() 只有这两项,数列
只有这两项,数列![]() 为有穷数列,但不存在某一项
为有穷数列,但不存在某一项![]() ,故②错误;
,故②错误;
当![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() ,数列不存在单调递增性,故③错误;
,数列不存在单调递增性,故③错误;
![]()
![]()
![]()
![]() ①
①
且![]() ②
②
①![]() ②得:
②得:![]()
令![]() ,则数列
,则数列![]() 是以
是以![]() 为公比的等比数列
为公比的等比数列
则![]()
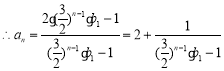
当![]() 时,
时,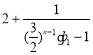 的极限为2,否则式子无意义,故④正确
的极限为2,否则式子无意义,故④正确
故答案为:①④

练习册系列答案
相关题目