题目内容
椭圆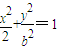 的焦点为F1,F2,两条准线与x轴的交点分别为M,N,若|MN|≤2|F1F2|,则该椭圆离心率取得最小值时的椭圆方程为 .
的焦点为F1,F2,两条准线与x轴的交点分别为M,N,若|MN|≤2|F1F2|,则该椭圆离心率取得最小值时的椭圆方程为 .
【答案】分析:由椭圆的性质及已知|MN|≤2|F1F2|,可得c的范围,进而可求离心率e最小时的c的值,求出b,即可求解椭圆的方程
解答:解:由题意可得|MN|=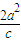 =
=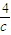 ,|F1F2|=2c,c2=2-b2
,|F1F2|=2c,c2=2-b2
∵|MN|≤2|F1F2|,
∴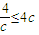
∴c≥1即离心率e=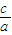 的最小值为
的最小值为
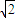 ,此时有c=1,b=1
,此时有c=1,b=1
∴椭圆方程为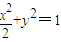
故答案为: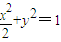
点评:本题主要考查了椭圆的性质在椭圆的标准方程的求解中的应用,解题的关键是寻求离心率e取得最小值时的a,c的关系
解答:解:由题意可得|MN|=
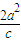 =
=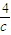 ,|F1F2|=2c,c2=2-b2
,|F1F2|=2c,c2=2-b2∵|MN|≤2|F1F2|,
∴
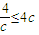
∴c≥1即离心率e=
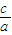 的最小值为
的最小值为
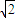 ,此时有c=1,b=1
,此时有c=1,b=1∴椭圆方程为
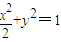
故答案为:
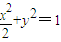
点评:本题主要考查了椭圆的性质在椭圆的标准方程的求解中的应用,解题的关键是寻求离心率e取得最小值时的a,c的关系

练习册系列答案
相关题目
