题目内容
若直线y=x-m与曲线y=
有两个不同的交点,则实数m的取值范围是
| 1-x2 |
(-
,-1)
| 2 |
(-
,-1)
.| 2 |
分析:y=
有两个表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,把斜率是1的直线平行移动,即可求得结论
| 1-x2 |
解答: 解:∵y=
解:∵y=
表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分.
作出曲线y=
的图象,在同一坐标系中,再作出直线y=x-m,平移过程中,直线先与圆相切,再与圆有两个交点,
直线与曲线相切时,可得,
=1
∴m=-
当直线y=x-m经过点(-1,0)时,m=-1,直线y=x+1,而该直线也经过(0,1),即直线y=x+1与半圆有2个交点
故答案为:(-
,-1)
 解:∵y=
解:∵y=| 1-x2 |
作出曲线y=
| 1-x2 |
直线与曲线相切时,可得,
| |-m| | ||
|
∴m=-
| 2 |
当直线y=x-m经过点(-1,0)时,m=-1,直线y=x+1,而该直线也经过(0,1),即直线y=x+1与半圆有2个交点
故答案为:(-
| 2 |
点评:本题考查直线与曲线的交点问题,在同一坐标系中,分别作出函数的图象,借助于数形结合是求解的关键

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
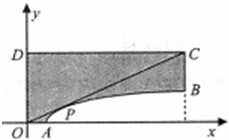 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组