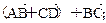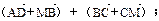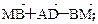题目内容
若点M是 所在平面内的一点,且满足
所在平面内的一点,且满足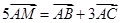 ,则
,则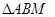 与
与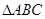 的面积比为( )
的面积比为( )
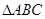 所在平面内的一点,且满足
所在平面内的一点,且满足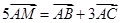 ,则
,则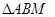 与
与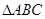 的面积比为( )
的面积比为( )A.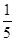 | B.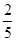 | C.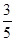 | D.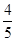 |
C
M是△ABC所在平面内一点,连接AM,BM,延长AC至D使AD=3AC,延长AM至E使AE=5AM.
∵5 =
=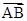 +3
+3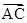 ,
,
∴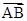 =5
=5 -3
-3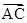 =
=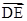 ,
,
连接BE,则四边形ABED是平行四边形(向量AB和向量DE平行且模相等)
由于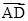 =3
=3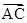 ,所以三角形ABC面积=
,所以三角形ABC面积=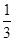 三角形ABD面积
三角形ABD面积
 =
=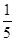
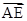
,所以三角形AMB面积=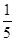 三角形ABE面积
三角形ABE面积
在平行四边形中,三角形ABD面积=三角形ABE面积=平行四边形ABED面积一半
故△ABM与△ABC的面积比=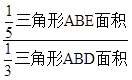 =
=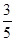 故选C.
故选C.
∵5
 =
=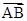 +3
+3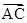 ,
,∴
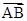 =5
=5 -3
-3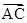 =
=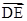 ,
,连接BE,则四边形ABED是平行四边形(向量AB和向量DE平行且模相等)
由于
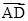 =3
=3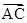 ,所以三角形ABC面积=
,所以三角形ABC面积=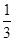 三角形ABD面积
三角形ABD面积 =
=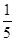
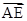
,所以三角形AMB面积=
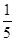 三角形ABE面积
三角形ABE面积在平行四边形中,三角形ABD面积=三角形ABE面积=平行四边形ABED面积一半
故△ABM与△ABC的面积比=
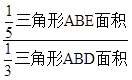 =
=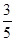 故选C.
故选C.
练习册系列答案
相关题目
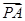 ,
,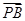 ,
,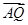 ,
,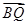 满足如下条件:
满足如下条件: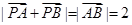 ;
;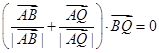 ;③
;③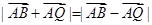 ,则
,则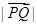 的最大值与最小值之差是( )
的最大值与最小值之差是( )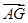 =λ
=λ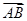 +μ
+μ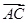 (λ,μ∈R),若∠A=120°,
(λ,μ∈R),若∠A=120°,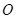 为
为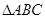 的外心,以线段
的外心,以线段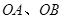 为邻边作平行四边形,第四个顶点为
为邻边作平行四边形,第四个顶点为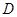 ,再以
,再以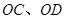 为邻边作平行四边形,它的第四个顶点为
为邻边作平行四边形,它的第四个顶点为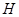 .
.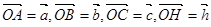 ,试用
,试用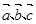 表示
表示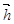 ;
;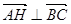 ;
;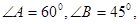 外接圆的半径为
外接圆的半径为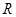 ,用
,用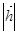 .
.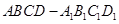 中,
中,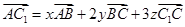 ,
,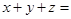 ( )
( ) .1
.1  .
.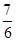
 .
. 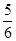
 .
.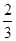
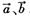 不共线,若
不共线,若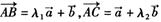 ,且A、B、C三点共线,则关于实数
,且A、B、C三点共线,则关于实数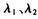 一定成立的关系式为( )
一定成立的关系式为( ) ="1" B.
="1" B.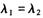 =" -1" C.
=" -1" C.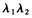 ="1" D.
="1" D.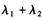 =1
=1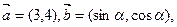 且
且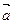 ∥
∥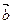 ,则
,则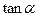 =( )
=( )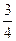
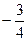
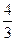
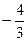
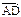 的是( )
的是( )