题目内容
已知实系数方程x2+ax+2b=0的两根在(0,1)与(1,2)内，求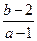
的取值范围.
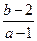的取值范围.∴
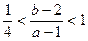
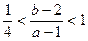
设f(x)=x2+ax+2b,依题意,此函数图象与x轴两交点横坐标在(0,1)和(1,2)内,其充要条件为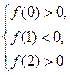
即
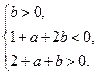
在直角坐标系中作出可行域,如下图所示.
由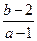的几何意义知△ABC内任一点P(a,b)与定点M(1,2)连线的斜率的范围即为所求.
∵
,
∴
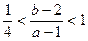
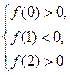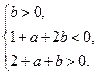
即在直角坐标系中作出可行域,如下图所示.
由
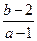的几何意义知△ABC内任一点P(a,b)与定点M(1,2)连线的斜率的范围即为所求.∵
, ∴
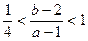
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
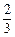，预期目标为两企业年利润之和为160万元，以2006年初起．
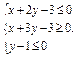若目标函数z=ax+y(其中a＞0)仅在点（3，0）处取得最大值，求a的取值范围.
与连接
两点的线段有交点，求实数
的取值范围．
、
两种型号的帐篷中选择一种，
顶，用不等式将题目中的不等关系表示出来．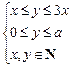
的有序数对
为“和谐格点”，则当
时，和谐格点的个数是 ．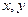
满足条件
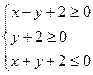，那么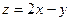
的最小值为 .
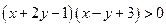表示的平面区域．