题目内容

设向量a=（
1
2
，sina）的模为
2
2
，则cos2a=
1
2
1
2
．
分析：由题意，利用向量的模的计算公式列出关系式，得到sin2α的值，然后把所求的式子利用二倍角的余弦函数公式化简，将sin2α的值代入即可求出值．
解答：解：∵
a
=（
1
2
，sina）的模为
2
2
，
∴|
a
|=
(
1
2
)2+sin2α
=
2
2
，
∴sin2α=
1
4
，
则cos2a=1-2sin2α=1-2×
1
4
=
1
2
．
故答案为：
1
2
点评：此题考查了平面向量的模，以及二倍角的余弦函数公式，熟练掌握二倍角的余弦函数公式是解本题的关键．
练习册系列答案
相关题目
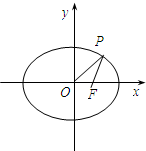如图，F为椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点，P为椭圆上一点，O为原点，记△OFP的面积为S，且
OF
•
FP
=1．
（1）设
1
2
＜S＜
3
2
，求向量
OF
与
FP
夹角的取值范围．
（2）设|
OF
|=c，S=
3
4
c，当c≥2时，求当|
OP
|取最小值时的椭圆方程．
已知锐角△ABC中的三个内角分别为A、B、C．
（1）设
BC
•
CA
=
CA
•
AB
，∠A=
5π
12
，求△ABC中∠B的大小；
（2）设向量
s
=(2sinC，  -
3
)，
t
=(cos2C，  2cos2
C
2
-1)，且
s
∥
t
，若sinA=
2
3
，求sin(
π
3
-B)的值．
（2008•成都三模）已知O为坐标原点，点E、F的坐标分别为（-
2
，0）、（
2
，0），点A、N满足
AE
=2
3
，
ON
=
1
2
(
OA
+
OF
)，过点N且垂直于AF的直线交线段AE于点M，设点M的轨迹为C．
（1）求轨迹C的方程；
（2）若轨迹C上存在两点P和Q关于直线l：y=k（x+1）（k≠0）对称，求k的取值范围；
（3）在（2）的条件下，设直线l与轨迹C交于不同的两点R、S，对点B（1，0）和向量a=（-
3
，3k），求
BR
•
BS
-|a|2取最大值时直线l的方程．
已知锐角△ABC中的三个内角分别为A、B、C．
（1）设
BC
•
CA
=
CA
•
AB
，∠A=
5π
12
，求△ABC中∠B的大小；
（2）设向量
s
=(2sinC，  -
3
)，
t
=(cos2C，  2cos2
C
2
-1)，且
s
∥
t
，若sinA=
2
3
，求sin(
π
3
-B)的值．
如图，F为椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点，P为椭圆上一点，O为原点，记△OFP的面积为S，且
OF
•
FP
=1．
（1）设
1
2
＜S＜
3
2
，求向量
OF
与
FP
夹角的取值范围．
（2）设|
OF
|=c，S=
3
4
c，当c≥2时，求当|
OP
|取最小值时的椭圆方程．
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网