题目内容
如图,F为椭圆
+
=1(a>b>0)的右焦点,P为椭圆上一点,O为原点,记△OFP的面积为S,且
•
=1.
(1)设
<S<
,求向量
与
夹角的取值范围.
(2)设|
|=c,S=
c,当c≥2时,求当|
|取最小值时的椭圆方程.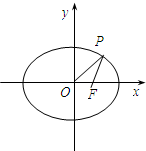
| x2 |
| a2 |
| y2 |
| b2 |
| OF |
| FP |
(1)设
| 1 |
| 2 |
| ||
| 2 |
| OF |
| FP |
(2)设|
| OF |
| 3 |
| 4 |
| OP |

(1)设
与
的夹角为θ,由题意得
•
=|
|•|
|cosθ=1,S=
|
|•|
|sin(π-θ)…(2分)
两式相除可得tanθ=2S,又
<S<
,所以1<tanθ<
…(2分)
所以向量
与
夹角的取值范围是45°<θ<60°…(1分)
(2)设P(x0,y0),F(c,0),所以
=(c,0),
=(x0-c,y0),
所以
•
=c(x0-c)=1,即x0=c+
…(1分)
所以S=
c|y0|=
c,|y0|=
…(1分)
所以|
|=
=
…(2分)
由单调性可知当c=2时有最小值,此时x0=
,…1分|y0|=3,此时F1(-2,0),F2(2,0),所以2a=PF1+PF2=
+
=2
…(2分)
所以椭圆方程为
+
=1…(2分)
| OF |
| FP |
| OF |
| FP |
| OF |
| FP |
| 1 |
| 2 |
| OF |
| FP |
两式相除可得tanθ=2S,又
| 1 |
| 2 |
| ||
| 2 |
| 3 |
所以向量
| OF |
| FP |
(2)设P(x0,y0),F(c,0),所以
| OF |
| FP |
所以
| OF |
| FP |
| 1 |
| c |
所以S=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
所以|
| OP |
|
(c+
|
由单调性可知当c=2时有最小值,此时x0=
| 5 |
| 2 |
(
|
(
|
| 10 |
所以椭圆方程为
| x2 |
| 10 |
| y2 |
| 6 |

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
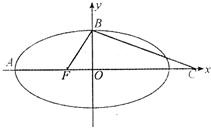 如图,F是椭圆
如图,F是椭圆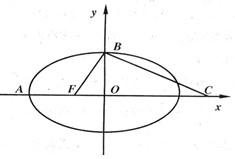 如图,F是椭圆
如图,F是椭圆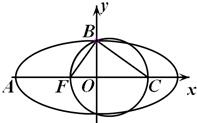 如图,F是椭圆
如图,F是椭圆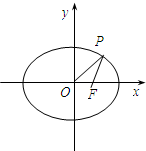 如图,F为椭圆
如图,F为椭圆