题目内容
如果实数x，y满足
，对任意的正数a，b，不等式ax+by≤1恒成立，则a+b的取值范围是（ ）
|
A、(0，
| ||
| B、（0，4] | ||
C、[
| ||
| D、（0，2） |
分析：画出不等式组表示的平面区域，判断出区域的形状，求出a，b的范围，进一步求出a+b的范围．
解答：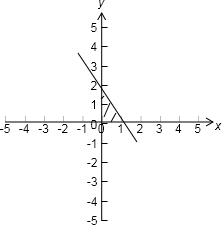
解：画出不等式组表示的平面区域
由题意．x，y所形成区域是由（0，0）．（1，0）．（0，2）三点围成的三角形．
因以为ax+by≤1恒成立所以a≤1．b≤
．所以a+b≤
；
所以a+b的取值范围是（0，
]
故选A
解：画出不等式组表示的平面区域由题意．x，y所形成区域是由（0，0）．（1，0）．（0，2）三点围成的三角形．
因以为ax+by≤1恒成立所以a≤1．b≤
| 1 |
| 2 |
| 3 |
| 2 |
所以a+b的取值范围是（0，
| 3 |
| 2 |
故选A
点评：利用线性规划求函数的最值，关键是画出不等式组表示的平面区域，给函数赋予几何意义．
练习册系列答案
阅读快车系列答案
相关题目