题目内容
11．如图所示，两轮半径分别是（A、B、C、D分别是切点）25cm和5cm，轴心距O1O2=40cm，求接两轮的传动皮带的长．
分析 皮带长=圆O1上两个切点左边的弧长+2AB+圆O2上两个切点右边的弧长．
解答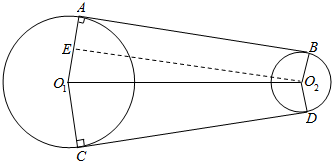 
解：∵两个皮带轮的半径分别为70cm和20cm，
∴O1E=20cm，
圆心距O1O2=40cm，
∴AB=EO2=20$\sqrt{3}$cm，
∠AO1O2=60°，
∴皮带长为=$\frac{4}{3}π×25$+$\frac{2π}{3}×5$+20$\sqrt{3}$×2=$\frac{110}{3}$π+40$\sqrt{3}$（cm）．
点评 考查了弧长的计算，切线的性质，勾股定理，本题关键是根据勾股定理求得AB的长，即求出∠AO1O2的度数．
练习册系列答案
相关题目
19．一条直线不与坐标轴平行或重合，则它的方程（ ）
| A． | 可以写成两点式或截距式 | B． | 可以写成两点式或斜截式或点斜式 | ||
| C． | 可以写成点斜式或截距式 | D． | 可以写成两点式或截距式或点斜式 |
6．已知椭圆的上顶点和左焦点都在直线y=2x+2上，则这一椭圆的标准方程是（ ）
| A． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{4}$=1 | B． | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{2}$=1 | C． | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1 | D． | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{2}$=1 |