题目内容
【题目】已知椭圆![]() 中心在坐标原点,焦点在
中心在坐标原点,焦点在![]() 轴上,且过
轴上,且过![]() ,直线
,直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 两点不是左右顶点),若直线
两点不是左右顶点),若直线![]() 的斜率为
的斜率为![]() 时,弦
时,弦![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若以![]() ,
,![]() 两点为直径的圆过椭圆的右顶点,则直线
两点为直径的圆过椭圆的右顶点,则直线![]() 是否经过定点,若是,求出定点坐标,若不是,请说明理由.
是否经过定点,若是,求出定点坐标,若不是,请说明理由.
【答案】(1) 椭圆的方程为:![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据斜率公式以及中点坐标公式得![]() ,
,![]() ,再由椭圆的标准方程利用点差法得
,再由椭圆的标准方程利用点差法得![]() ,因此可得
,因此可得![]() ,最后与
,最后与![]() 在椭圆上联立方程组解得
在椭圆上联立方程组解得![]() ,(2)根据以
,(2)根据以![]() ,
,![]() 两点为直径的圆过椭圆的右顶点,得
两点为直径的圆过椭圆的右顶点,得![]() ,设直线方程,与椭圆方程联立,利用韦达定理代入化简得
,设直线方程,与椭圆方程联立,利用韦达定理代入化简得![]() ,解得
,解得![]() 或
或![]() ,即得定点,最后验证斜率不存在的情形也满足.
,即得定点,最后验证斜率不存在的情形也满足.
(Ⅰ)设椭圆的标准方程为![]() ,
,![]() ,
,![]()
由题意直线![]() 的斜率为
的斜率为![]() ,弦
,弦![]() 的中点
的中点![]() 在直线
在直线![]() 上,得
上,得![]() ,
,![]() ,
,
再根据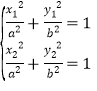 作差变形得
作差变形得 ![]() ,所以
,所以![]() ,又因为椭圆过
,又因为椭圆过![]() 得到
得到![]() ,
,
所以椭圆的方程为:![]() .
.
(Ⅱ)由题意可得椭圆右顶点![]() ,
,![]()
⑴当直线![]() 的斜率不存在时,设直线
的斜率不存在时,设直线![]() 的方程为
的方程为![]() ,此时要使以
,此时要使以![]() ,
,![]() 两点为直径的圆过椭圆的右顶点则有以
两点为直径的圆过椭圆的右顶点则有以![]() 解得
解得![]() 或
或![]() (舍)此时直线
(舍)此时直线![]() 为
为![]()
⑵当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,则有
,则有![]() ,
,
化简得![]() ①
①
联立直线和椭圆方程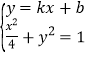 得
得![]() ,
,
![]() ,
, ![]() ②
②
把②代入①得![]()
即![]()
![]() ,得
,得![]() 或
或![]() 此时直线
此时直线![]() 过
过![]() 或
或![]() (舍)
(舍)
综上所述直线![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目