题目内容
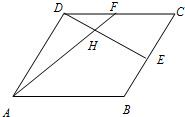在边长为1的菱形ABCD中，∠ABC=120°，E、F分别是BC、CD的中点，DE交AF于点H，则| AH |
| AB |
分析：本题考查的知识点是平面向量的数量积运算，由已知在边长为1的菱形ABCD中，∠ABC=120°我们易得向量
•
及
2的值，，故我们只要能将向量
用向量
与
表示，即可求解．
| AB |
| AD |
| AB |
| AH |
| AB |
| AD |
解答：解：设
=t
=t(
+
)=t
+
又由D，H，E三点共线，则可设：
=μ
+(1-μ)
=μ
+(1-μ)(
+
)
=(
+
)
+(1-μ)
即：
解得：t=
∴
=
+
∴
•
=（
+
）•
=
•
+
=
故答案为：
| AH |
| AF |
| AD |
| 1 |
| 2 |
| AB |
| AD |
| t |
| 2 |
| AB |
又由D，H，E三点共线，则可设：
| AH |
| AD |
| AE |
=μ
| AD |
| AB |
| 1 |
| 2 |
| AD |
=(
| 1 |
| 2 |
| μ |
| 2 |
| AD |
| AB |
即：
|
解得：t=
| 4 |
| 5 |
∴
| AH |
| 4 |
| 5 |
| AD |
| 2 |
| 5 |
| AB |
∴
| AH |
| AB |
| 4 |
| 5 |
| AD |
| 2 |
| 5 |
| AB |
| AB |
=
| 4 |
| 5 |
| AD |
| AB |
| 2 |
| 5 |
| AB2 |
=
| 4 |
| 5 |
故答案为：
| 4 |
| 5 |
点评：若
= λ
+μ
，且λ+μ=1．则A、B、C三点共线，且C分AB的两段线段AC与BC的长度之比，AC：BC=μ：λ
| OC |
| OA |
| OB |
练习册系列答案
名校课堂系列答案
相关题目
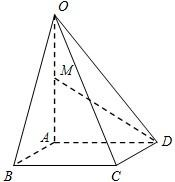如图，在四棱锥O-ABCD中，底面ABCD是边长为1的菱形，
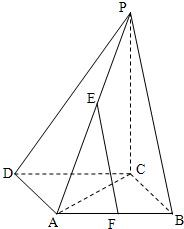如图，在边长为a的菱形ABCD中，∠ABC=60°，PC⊥面ABCD，E，F是PA和AB的中点．在四棱锥P-ABCD中，底面是边长为1的菱形，∠ABC=60°，PA⊥底面ABCD，PA=1，则异面直线AB与PD所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在边长为1的菱形ABCD中（如图），|