Question

在四棱锥P-ABCD中，底面是边长为1的菱形，∠ABC=60°，PA⊥底面ABCD，PA=1，则异面直线AB与PD所成角的余弦值为（　　）

• A、

  2

  4

• B、

  14

  4

• C、

  2

  2

• D、

  2

  3

Answer 1

分析：取CD的中点E，连接AE，由底面是边长为1的菱形，∠ABC=60°，PA⊥底面ABCD，PA=1，我们可以建立如图所示的空间坐标系，分别求出异面直线AB与PD的方向向量，代入向量夹角公式，即可求出异面直线AB与PD所成角的余弦值．

解答：解：取CD的中点E，连接AE，由底面是边长为1的菱形，∠ABC=60°，可得AB⊥AE
以A为坐标原点建立如图所示的坐标系

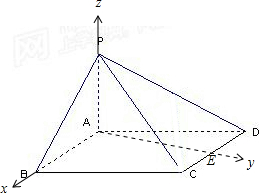
则

AB

=（1，0，0），

PD

=（-

1

2

，

3

2

，-1）
设异面直线AB与PD所成角为θ
则cosθ=|

AB • PD

| AB |•| PD |

|=

2

4

故选A

点评：本题考查的知识点是异面直线及其所成的角，其中建立坐标系，将空间直线与直线的夹角问题转化为向量夹角问题是解答本题的关键．