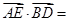题目内容
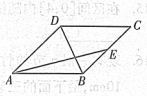
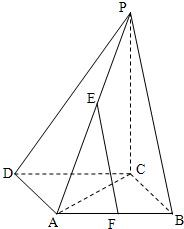 如图,在边长为a的菱形ABCD中,∠ABC=60°,PC⊥面ABCD,E,F是PA和AB的中点.
如图,在边长为a的菱形ABCD中,∠ABC=60°,PC⊥面ABCD,E,F是PA和AB的中点.(1)求证:EF||平面PBC;
(2)求E到平面PBC的距离.
分析:(1)欲证EF∥平面PBC,根据直线与平面平行的判定定理可知只需证EF与平面PBC内一直线平行,而EF∥PB,又EF?平面PBC,PB?平面PBC,满足定理所需条件;
(2)在面ABCD内作过F作FH⊥BC于H,又EF∥平面PBC,故点E到平面PBC的距离等于点F到平面PBC的距离FH.在直角三角形FBH中,求出FH即可,最后根据点E到平面PBC的距离等于点F到平面PBC的距离即可求出所求.
(2)在面ABCD内作过F作FH⊥BC于H,又EF∥平面PBC,故点E到平面PBC的距离等于点F到平面PBC的距离FH.在直角三角形FBH中,求出FH即可,最后根据点E到平面PBC的距离等于点F到平面PBC的距离即可求出所求.
解答:(1)证明:∵AE=PE,AF=BF,
∴EF∥PB
又EF?平面PBC,PB?平面PBC,
故EF∥平面PBC;
(2)解:在面ABCD内作过F作FH⊥BC于H
∵PC⊥面ABCD,PC?面PBC
∴面PBC⊥面ABCD
又面PBC∩面ABCD=BC,FH⊥BC,FH?面ABCD∴FH⊥面PBC
又EF||平面PBC,故点E到平面PBC的距离等于点F到平面PBC的距离FH.
在直角三角形FBH中,∠FBC=60°,FB=
,FH=FBsin∠FBC=
×sin60°=
×
=
a,
故点E到平面PBC的距离等于点F到平面PBC的距离,
等于
a.
∴EF∥PB
又EF?平面PBC,PB?平面PBC,
故EF∥平面PBC;
(2)解:在面ABCD内作过F作FH⊥BC于H
∵PC⊥面ABCD,PC?面PBC
∴面PBC⊥面ABCD
又面PBC∩面ABCD=BC,FH⊥BC,FH?面ABCD∴FH⊥面PBC
又EF||平面PBC,故点E到平面PBC的距离等于点F到平面PBC的距离FH.
在直角三角形FBH中,∠FBC=60°,FB=
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
| ||
| 4 |
故点E到平面PBC的距离等于点F到平面PBC的距离,
等于
| ||
| 4 |
点评:本题主要考查了直线与平面平行的判定,以及点到平面的距离,同时考查了空间想象能力,以及转化与划归的思想,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 (2013•潍坊一模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为BC中点,则
(2013•潍坊一模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为BC中点,则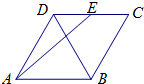 (2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则
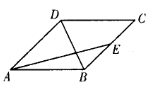
(2013•昌平区二模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为CD的中点,则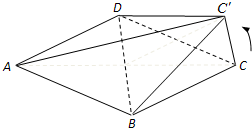 如图,在边长为1的菱形ABCD中,将正三角形BCD沿BD向上折起,折起后的点C记为C′,且CC′=a(
如图,在边长为1的菱形ABCD中,将正三角形BCD沿BD向上折起,折起后的点C记为C′,且CC′=a(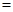
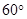 ,
,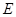 为
为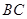 的中点,则
的中点,则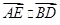
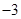 B.
B.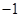 C.
C. D.
D.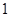
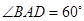 , E为BC中点,则
, E为BC中点,则