题目内容
【题目】已知双曲线C: ![]() =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ![]() ,实轴长为2,直线l:x﹣y+m=0与双曲线C交于不同的两点A,B,
,实轴长为2,直线l:x﹣y+m=0与双曲线C交于不同的两点A,B,
(1)求双曲线C的方程;
(2)若线段AB的中点在圆x2+y2=5上,求m的值;
(3)若线段AB的长度为4 ![]() ,求直线l的方程.
,求直线l的方程.
【答案】
(1)解:由题意,得 ![]() =
= ![]() ,2a=2,又因为c2=a2+b2
,2a=2,又因为c2=a2+b2
解得a=1,c= ![]() ,
,
∴b2=c2﹣a2=2
∴所求双曲线C的方程为x2﹣ ![]() =1
=1
(2)解:设A、B两点的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y0),
由 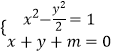 得x2﹣2mx﹣m2﹣2=0,判别式△>0,
得x2﹣2mx﹣m2﹣2=0,判别式△>0,
∴x0= ![]() =m,y0=x0+m=2m,
=m,y0=x0+m=2m,
∵点M(x0,y0)在圆x2+y2=5上,
∴m2+(2m)2=5,
∴m=±1
(3)解:由 ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =4
=4 ![]()
解得m=±2
所以直线l的方程为x﹣y+2=0或x﹣y﹣2=0
【解析】(1)根据双曲线的离心率和和实轴长即可求出a,b的值,问题得以解决,(2)设A、B两点的坐标分别为(x1 , y1),(x2 , y2),线段AB的中点为M(x0 , y0),根据点M(x0 , y0)在圆x2+y2=5上,即可求出m的值,(3)根据弦长公式即可求出m的值.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】某工厂36名工人年龄数据如图:
工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 | 工人编号 | 年龄 |
1 | 40 | 10 | 36 | 19 | 27 | 28 | 34 |
(1)用系统抽样法从36名工人中抽取容量为9的样本,且在第一分段里用随机抽样法抽到的年龄数据为44,列出样本的年龄数据;
(2)计算(1)中样本的均值 ![]() 和方差s2;
和方差s2;
(3)36名工人中年龄在 ![]() ﹣s和
﹣s和 ![]() +s之间有多少人?所占百分比是多少(精确到0.01%)?
+s之间有多少人?所占百分比是多少(精确到0.01%)?