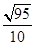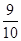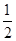题目内容
定义在R上的函数f(x)满足f(-x)=-f(x),f(x-2)=f(x+2),且x∈(-1,0)时,f(x)=2x+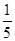 ,则f(log220)的值为( )
,则f(log220)的值为( )
| A.1 | B.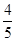 | C.-1 | D.-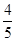 |
C
解析

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
已知函数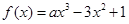 ,若
,若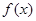 存在唯一的零点
存在唯一的零点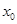 ,且
,且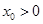 ,则
,则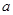 的取值范围是
的取值范围是
A.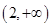 | B.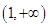 | C.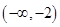 | D.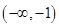 |
已知函数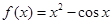 ,则
,则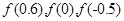 的大小关系是( )
的大小关系是( )
A.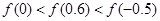 |
B.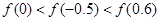 |
C.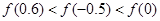 |
D.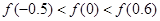 |
定义在R上的函数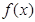 和
和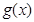 的导函数分别为
的导函数分别为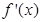 ,
,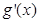 ,则下面结论正确的是( )
,则下面结论正确的是( )
①若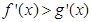 ,则函数
,则函数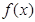 的图象在函数
的图象在函数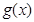 的图象上方;
的图象上方;
②若函数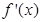 与
与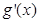 的图象关于直线
的图象关于直线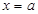 对称,则函数
对称,则函数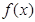 与
与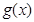 的图象关于点(
的图象关于点(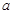 ,0)对称;
,0)对称;
③函数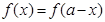 ,则
,则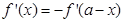 ;
;
④若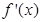 是增函数,则
是增函数,则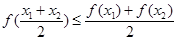 .
.
| A.①② | B.①②③ | C.③④ | D.②③④ |
(3分)(2011•重庆)已知 ,则a=( )
,则a=( )
| A.1 | B.2 | C.3 | D.6 |
函数f(x)=lnx-x-a有两个不同的零点,则实数a的取值范围是( )
| A.(-∞,-1] | B.(-∞,-1) |
| C.[-1,+∞) | D.(-1,+∞) |
f(x)的定义域为R,且f(x)=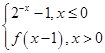 ,若方程f(x)=x+a有两个不同实根,则a的取值范围为( )
,若方程f(x)=x+a有两个不同实根,则a的取值范围为( )
| A.(-∞,1) | B.(-∞,1] |
| C.(0,1) | D.(-∞,+∞) |
若函数f(x)、g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=ex,则有( )
| A.f(2)<f(3)<g(0) | B.g(0)<f(3)<f(2) |
| C.f(2)<g(0)<f(3) | D.g(0)<f(2)<f(3) |
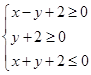 内一点
内一点 作圆
作圆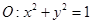 的两条切线,切点分别为
的两条切线,切点分别为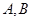 ,记
,记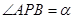 ,则当
,则当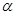 最小时
最小时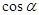 的值为( )
的值为( )