题目内容
【题目】2019年全国“两会”，即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国会第二次会议，分别于2019年3月5日和3月3日在北京召开．为了了解哪些人更关注“两会”，某机构随机抽取了年龄在
岁之间的200人进行调查，并按年龄绘制出频率分布直方图，如图．
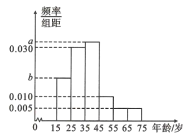
若把年龄在区间
，
内的人分别称为“青少年”“中老年”．经统计“青少年”和“中老年”的人数之比为
．其中“青少年”中有40人关注“两会”，“中老年”中关注“两会”和不关注“两会”的人数之比为
．
（1）求图中
的值．
（2）现采用分层抽样在
和
中随机抽取8人作为代表，从8人中任选2人，求2人都是“中老年”的概率．
（3）根据已知条件，完成下面的
列联表，并判断能否有
％的把握认为“中老年”比“青少年”更加关注“两会”．
关注 | 不关注 | 总计 | |
“青少年” | |||
“中老年” | |||
总计 |
附：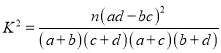
，其中
．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】（1）0.05；（2）
；（3）列联表见解析；有99.9%的把握认为“中老年”比“青少年”更加关注“两会”
【解析】
（1）由“青少年”和“中老年”的人数之比为
，求出
和
，即可得到
的值；
（2）由分层抽样求出在
中抽取6人，在
中抽取2人，再由古典概型求出2人都是“中老年”的概率即可；
（3）先求出
列联表，再由公式计算出
，比较即可得到结果.
（1）由题意得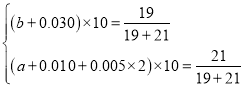
，
解得
，
所以
；
（2）由题意得，在中抽取
（人），
分别记为
，
，
，
，
，
，
在中抽取
（人），分别记为，．
则从8人中任选2人的全部基本事件有
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共28种，其中所选的2人都是“中老年”的事件只有这1种，
故2人都是“中老年”的概率；
（3）由题意得，抽取的200人中“青少年”共有
（人），
所以不关注两会的“青少年”共有
（人），
“中老年”中关注两会的人有
（人），
“中老年”中不关注两会的人有
（人），
所以列联表如下：
关注 | 不关注 | 总计 | |
“青少年” | 40 | 55 | 95 |
“中老年” | 70 | 35 | 105 |
总计 | 110 | 90 | 200 |
所以
，
所以有99.9%的把握认为“中老年”比“青少年”更加关注“两会”.
