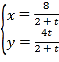题目内容
【题目】给定椭圆![]()
![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
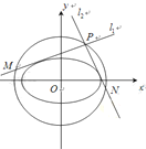
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的动点,过点
的“准圆”上的动点,过点![]() 作椭圆的切线
作椭圆的切线![]() 交“准圆”于点
交“准圆”于点![]() .
.
①当点![]() 为“准圆”与
为“准圆”与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 的方程并证明
的方程并证明![]() ;
;
②求证:线段![]() 的长为定值.
的长为定值.
【答案】(1)椭圆方程为![]() ,准圆方程为
,准圆方程为![]() ;(2)①
;(2)①![]() ,证明见解析;②证明见解析
,证明见解析;②证明见解析
【解析】
(1)根据题意![]() ,得到椭圆方程和准圆方程.
,得到椭圆方程和准圆方程.
(2)(ⅰ)设直线为![]() ,联立方程计算
,联立方程计算![]() 得到
得到![]() ,得到答案.
,得到答案.
(ⅱ)考虑斜率存在和不存在两种情况,设点![]() ,切线为
,切线为![]() ,联立方程得到
,联立方程得到![]() ,
,![]() ,得到直线
,得到直线![]() 垂直,得到线段
垂直,得到线段![]() 为准圆的直径,得到答案.
为准圆的直径,得到答案.
(1)![]() ,
,![]() 椭圆方程为
椭圆方程为![]() ,准圆方程为
,准圆方程为![]() .
.
(2)(ⅰ)因为准圆![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,
,
设过点![]() 且与椭圆相切的直线为
且与椭圆相切的直线为![]() ,
,
所以由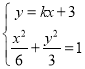 得
得![]() .
.
因为直线![]() 与椭圆相切,所以
与椭圆相切,所以![]() ,解得
,解得![]() ,
,
所以![]() 方程为
方程为![]() ,
,![]() ,
,![]() .
.
(ⅱ)①当直线![]() 中有一条斜率不存在时,不妨设直线
中有一条斜率不存在时,不妨设直线![]() 斜率不存在,
斜率不存在,
则![]() :
:![]() ,当
,当![]() :
:![]() 时,
时,![]() 与准圆交于点
与准圆交于点![]() ,
,
此时![]() 为
为![]() (或
(或![]() ),显然直线
),显然直线![]() 垂直;
垂直;
同理可证当![]() :
:![]() 时,直线
时,直线![]() 垂直
垂直
②当![]() 斜率存在时,设点
斜率存在时,设点![]() ,其中
,其中![]() .
.
设经过点![]() 与椭圆相切的直线为
与椭圆相切的直线为![]() ,
,
所以由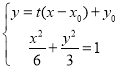 得
得![]() .
.
由![]() 化简整理得
化简整理得![]() ,
,
因为![]() ,所以有
,所以有![]() .
.
设![]() 的斜率分别为
的斜率分别为![]() ,因为
,因为![]() 与椭圆相切,
与椭圆相切,
所以![]() 满足上述方程
满足上述方程![]() ,
,
所以![]() ,即
,即![]() 垂直.
垂直.
综合①②知:因为![]() 经过点
经过点![]() ,又分别交其准圆于点
,又分别交其准圆于点![]() ,且
,且![]() 垂直.
垂直.
所以线段![]() 为准圆
为准圆![]() 的直径,
的直径,![]() ,
,
所以线段![]() 的长为定值6.
的长为定值6.

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.


由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年