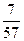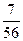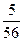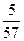题目内容
在等差数列{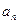 }中,
}中,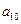 =18,前5项的和
=18,前5项的和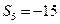
(1)求数列{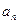 }的通项公式; (2)求数列{
}的通项公式; (2)求数列{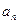 }的前
}的前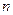 项和的最小值,并指出何时取最小.
项和的最小值,并指出何时取最小.
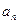 }中,
}中,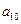 =18,前5项的和
=18,前5项的和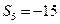
(1)求数列{
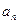 }的通项公式; (2)求数列{
}的通项公式; (2)求数列{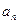 }的前
}的前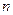 项和的最小值,并指出何时取最小.
项和的最小值,并指出何时取最小.(1)
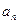 =3n-12
=3n-12(2)-18
解: (1)
得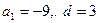 …………6分
…………6分 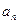 =3n-12…………8分
=3n-12…………8分
(2)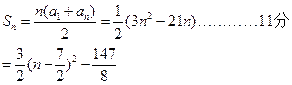 ∴
∴ 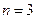 或4 …………13分
或4 …………13分
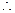 前n项的和取得最小值=-18…………15
前n项的和取得最小值=-18…………15
((2)另解:设前n项的和取得最小,则
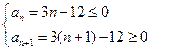
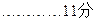
得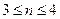 ∴
∴ 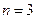 或4 …………13分
或4 …………13分
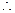 前n项的和取得最小值=-18…………15
前n项的和取得最小值=-18…………15

得
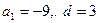 …………6分
…………6分 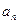 =3n-12…………8分
=3n-12…………8分(2)
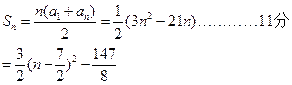 ∴
∴ 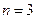 或4 …………13分
或4 …………13分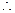 前n项的和取得最小值=-18…………15
前n项的和取得最小值=-18…………15((2)另解:设前n项的和取得最小,则

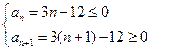
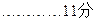
得
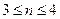 ∴
∴ 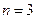 或4 …………13分
或4 …………13分 前n项的和取得最小值=-18…………15
前n项的和取得最小值=-18…………15
练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
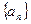 的前n项和为
的前n项和为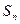 ,满足
,满足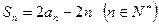
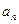
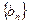 满足
满足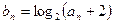 ,
,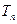 为数列
为数列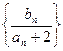 的前n项和,求证:
的前n项和,求证: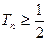
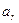 ,
,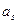 ,
,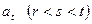 成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由。
成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由。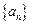 中,
中,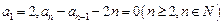 .
.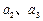 的值(只写结果),并求出数列
的值(只写结果),并求出数列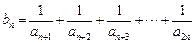 ,若对任意的正整数
,若对任意的正整数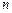 ,当
,当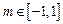 时,不等式
时,不等式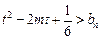 恒成立,求实数
恒成立,求实数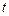 的取值范围。
的取值范围。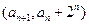 在直线
在直线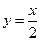 上,其中
上,其中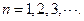
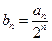 ,求证:数列
,求证:数列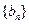 是等差数列;
是等差数列;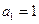 ,求数列
,求数列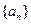 的前
的前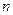 项和
项和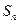 。
。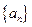 中,
中,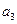 +
+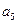 =12,那么
=12,那么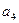 =" " ( )
=" " ( ) (n∈N*),若前n项的和为
(n∈N*),若前n项的和为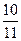 ,则项数
,则项数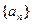 是等差数列,且
是等差数列,且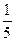
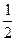
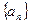 中,
中,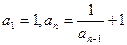 ,则
,则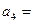 。
。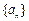 :
: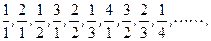 依它的前10项的规律,这个数列
依它的前10项的规律,这个数列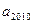 =( )
=( )